II. Méthodes chronométriques

II.1. Traces de fission

II.1.1. Introduction

L’utilisation des dommages créés dans les minéraux par la fission spontanée de l'uranium 238 (238U) a été proposée par Price et Walker à partir de 1963 pour dater les roches. Cette méthode découle de l’accumulation, au cours du temps, des traces de fission au sein du réseau cristallin dans les minéraux riches en uranium tels que l’apatite, le zircon, la titanite (Price et Walker, 1963 ; Fleischer et al., 1975).
L’estimation de l’âge s’effectue en déterminant la densité des traces spontanées dans ces minéraux. Les traces de fission sont stables selon une gamme de températures. A haute température, les traces sont détruites partiellement ou effacées de manière complète. Ce processus est observable par la mesure de la longueur des traces confinées, c'est-à-dire, situées à l’intérieur du cristal (Naeser, 1979 ; Gleadow et al., 1986 ; Green et al., 1989 ; Carlson, 1990 ; Corrigan, 1991 ; Crowley et al., 1991 ; Ketcham et al., 1999). Les mesures sont possibles seulement après un traitement chimique (attaque acide) approprié des cristaux.

Cette méthode a pris son essor depuis une vingtaine d’années et est utilisée dans une large variété de contexte géodynamique. Elle a été appliquée rapidement au problème d’exhumation des roches (Wagner et Reimer, 1972). L’analyse des traces de fission dans les cristaux d’apatite est une technique qui permet de déterminer leur histoire thermique à faible température (Brown et al., 1994 ; Gallagher et Brown, 1997 ; Gallagher et al., 1998 ; Gleadow et Brown, 2000). Les traces de fission sont par conséquent très utilisées pour rendre compte la dénudation et/ou l’exhumation  des reliefs (Brown et al., 1994). Les traces de fission étant sensibles à une certaine gamme de températures peuvent être utilisées pour déduire des profondeurs d’enfouissement en tenant compte du gradient géothermique d’une région donnée (en moyenne 30°C/km pour une lithosphère continentale stable). La sensibilité thermique des traces de fission à de faibles températures (< 110°C) fournit, de ce fait, un âge relatif inférieur aux âges stratigraphiques ou aux autres datations radiochronologiques. En effet, les datations déterminées par cette méthode fournissent des âges de refroidissement. Aussi, cette méthode apporte une contrainte significative sur l’évolution thermique d’une roche au cours du temps. A partir d’une histoire thermique ainsi reconstituée, il est possible de quantifier le taux d’érosion (Green et al., 1989 ; Gallagher et al., 1994 ; Fitzgerald et al., 1995). L’ampleur de l’érosion de la couverture sédimentaire ou encore l’évolution géodynamique d’une région peuvent être reconstituées (Gallagher et al., 1998).

Les traces de fission sont des outils permettant de quantifier la composante verticale des mouvements tectoniques qui ont pu affecter les premiers kilomètres de la croûte au cours des temps géologiques. Cette quantification s’opère au niveau des domaines orogéniques (étude des taux de surrection/érosion), dans les bassins sédimentaires, les socles anciens (érosion de "soubassement cristallin"), ainsi que dans les marges continentales (évolution géomorphologique). Dans les bassins sédimentaires, cette technique est largement utilisée pour la reconstitution de leur histoire thermique, la reconnaissance des épisodes d’inversions, ainsi que l’évaluation des paléogradients géothermiques (Wagner et Van den Haute, 1992 ; Armstrong et al., 1997 ; Gallagher et al., 1998). La thermochronologie TF est également appliquée dans l’exploration pétrolière où la probabilité de découvrir un gisement contenant de la matière organique mature dépend de l’histoire thermique et tectonique.

II.1.2. Principe de la méthode

La fission naturelle, correspondant à la fission spontanée, est produite par l’uranium 238 (238U). L’235U et le 232Th ont une période de fission trop importante pour que celle-ci soit mesurable à l’échelle des temps géologiques. La fission spontanée d’un atome d’238U libère deux atomes fils ionisés dits « fragments de fission » associés à quelques neutrons et une énergie atteignant environ 200 MeV. Cette dernière est exprimée sous la forme d’énergie cinétique (Ec).

Etant donnée la faible abondance isotopique de l’235U (0,7%) et sa période de désintégration par fission spontanée supérieure à l’238U, sa contribution à la formation des traces de fission spontanée est négligeable (<1/10000 par rapport à l’238U). Néanmoins, cet isotope possède la propriété de fissionner par capture neutronique, ce qui est indispensable pour la technique de datation par traces de fission.

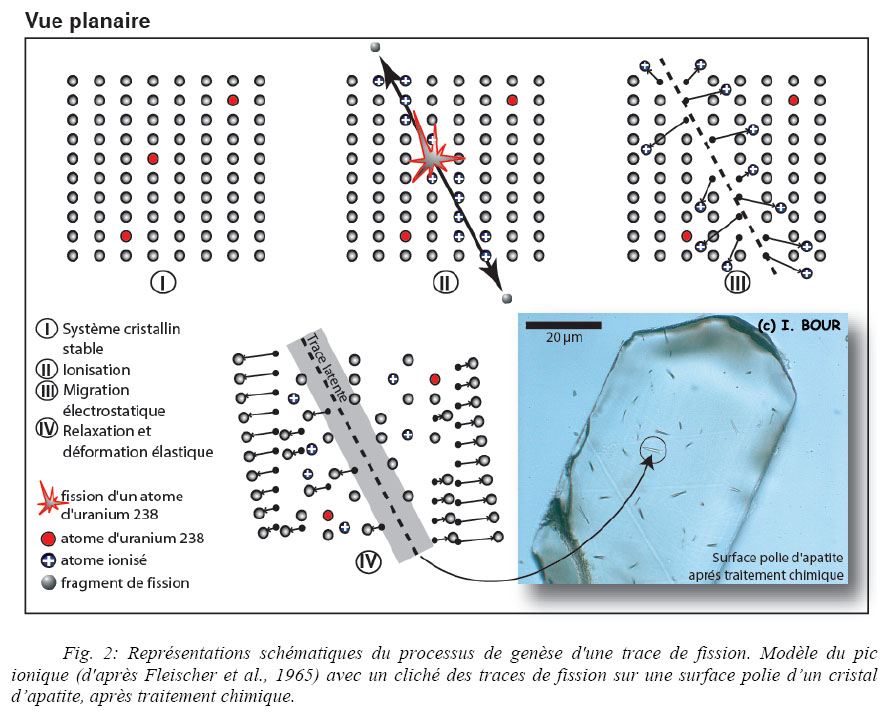
Les "fragments de fission" générés sont propulsés dans des directions opposées dans le minéral (Fig. 2). Les fragments de fission chargés perdent leur énergie en traversant la matière selon essentiellement deux processus :
1. les forces électrostatiques entre un ion lourd énergétique qui se propage dans un milieu et les électrons qui entourent les noyaux des atomes de ce milieu peuvent conduire à l'arrachement d'un ou plusieurs électrons de leur orbite, c'est le processus d'ionisation.
2. les chocs interatomiques causés par le passage du fragment de fission peuvent induire un déplacement direct des atomes du milieu. Ce processus intervient de façon prépondérante pour des énergies d’1MeV, c'est à dire dans un domaine où les ions lourds ne donnent plus de traces révélables.
Les traces seraient essentiellement une conséquence des ionisations produites dans le milieu ambiant par les ions. La modélisation de ce phénomène est exprimée dans le modèle du «pic d'explosion ionique» (Fig. 2).

Ce phénomène de fission, induit selon le modèle de pic d’explosion ionique (Fleischer et al., 1965 ; Fleischer et al., 1975 : Fig. 2), provoque une désorganisation locale de la maille cristalline (création de défauts) engendrée par une interaction électrostatique avec les atomes environnants (Fig. 2-III) le long du trajet des fragments de fission. La conséquence de la répulsion électrostatique ainsi générée est la formation d’une aire linéaire déprimée en atomes, d’un diamètre très faible (inférieur à 10 nm) et d’une longueur maximale s’échelonnant sur environ quelques µm (suivant le pouvoir d’arrêt de l’espèce minérale).

La trace discrète produite est dite « trace latente  ». Ces traces s’accumulent dans le cristal au cours du temps. Le nombre de traces dans un cristal d’apatite donné dépend de plusieurs paramètres physiques et chimiques, dont les principaux sont la durée pendant laquelle ces traces se sont accumulées (Fig. 3) et la concentration en uranium.

Il existe plusieurs approches expérimentales pour réaliser une datation par traces de fission (Gleadow, 1981). Les datations réalisées dans cette étude sont toutes issues de la méthode du détecteur externe qui consiste à dater individuellement plusieurs cristaux d’une même espèce minérale. C’est la méthode qui est la plus couramment utilisée dans les laboratoires (Gleadow, 1981 ; Hurford 1990a). Elle est simple à mettre en œuvre, peu consommatrice en cristaux et peut être applicable pour des cristaux à section prismatique (Jonckheere et al., 1993). Cette méthode est indispensable lorsque les variations de concentration en uranium sont importantes d’un cristal à l’autre, notamment dans les roches sédimentaires détritiques où dans cette situation, chaque grain peut être porteur d’une histoire thermique spécifique (Gleadow et al., 1976 ; Hurford 1990a). Elle a l’avantage de permettre une datation grain par grain d’une même espèce minérale procurant une meilleure homogénéité de l’information contenue dans les traces de fission. Ces caractéristiques permettent de contourner le problème lié aux hétérogénéités chimiques potentielles des différents cristaux d’un échantillon.

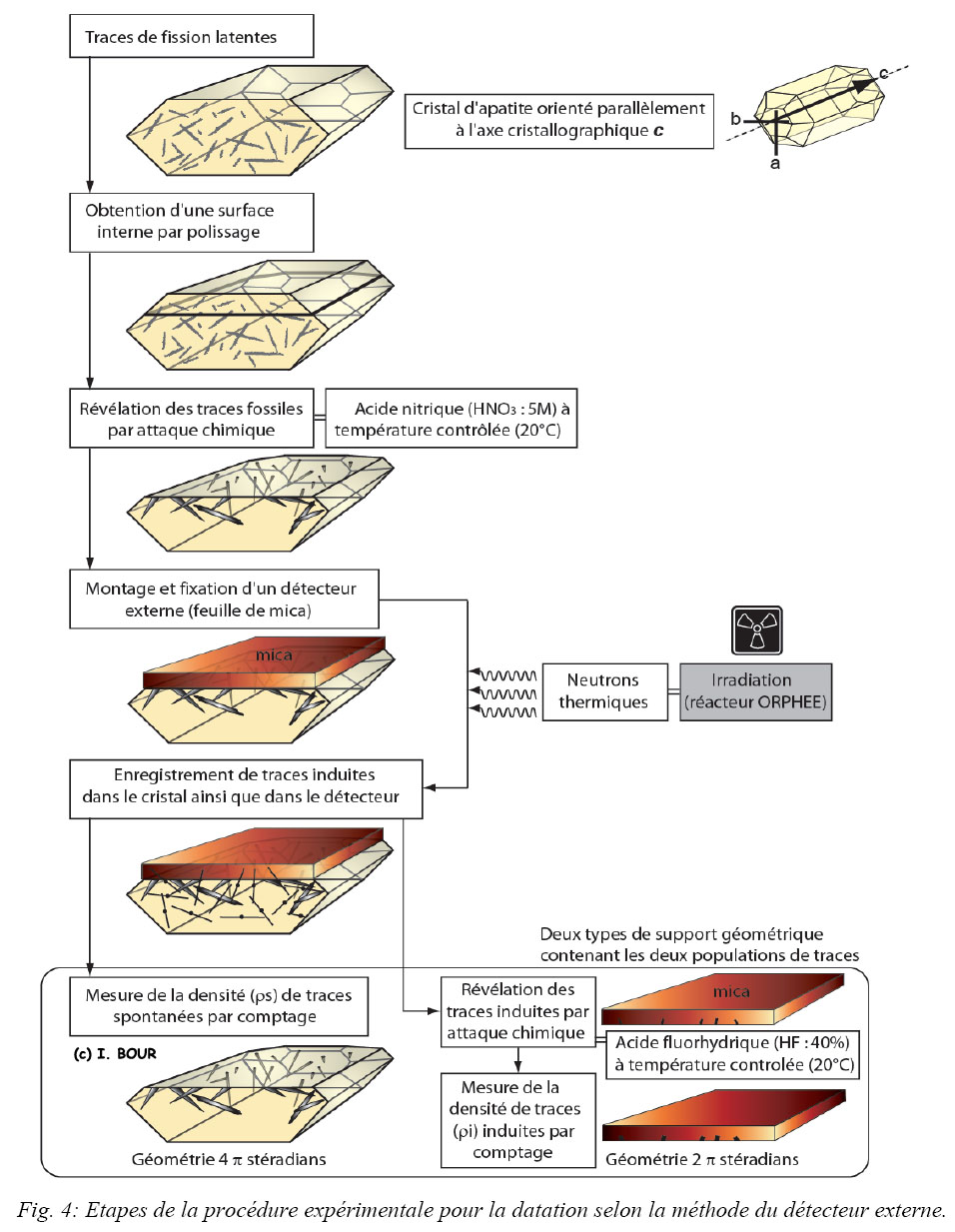
Du point de vue expérimental (Fig. 4), la méthode du détecteur externe consiste à polir et à traiter chimiquement l’ensemble des cristaux qui compose un échantillon. Cette surface polie est soumise à un traitement chimique nécessaire à la révélation des traces spontanées. Cette attaque chimique sélective, provoque l’élargissement de la section des traces par dissolution (révélation des traces) qui sont dès lors observables au microscope optique. Un détecteur externe (feuille de mica) est fixé sur le montage puis irradié conjointement. Les traces induites ainsi générées sont révélées à leur tour sur la feuille de mica.
Avec cette méthode, les traces spontanées et induites sont mesurées pour les mêmes grains. La mesure de ρi s’effectue sur un feuillet de mica qui a « enregistré » le processus de fission induite dans le cristal. Il est disposé à la surface du cristal (détecteur externe irradié conjointement avec le cristal puis soumis à un traitement acide).

Le protocole de séparation des cristaux d’apatite et la préparation des échantillons sont présentés dans le détail en Annexe 1.

II.1.3. Analyse des traces de fission

II.1.3.1. Révélation des traces de fission spontanées

De part leur diamètre très faible (quelques nm), les traces de fission fossiles ne sont pas directement observables au microscope optique (Price et Walker, 1962b). Un traitement par une solution acide est nécessaire afin de les « révéler » (dissolution de la surface). Tant que l’étape de révélation chimique des cristaux n’est pas effectuée, les traces sont dites « traces latentes ». L’agent acide réagit sur l’ensemble de la surface en contact et préférentiellement sur les traces latentes qui constituent des sites d’attaques favorables car elles sont chimiquement plus réactives que le reste du minéral.

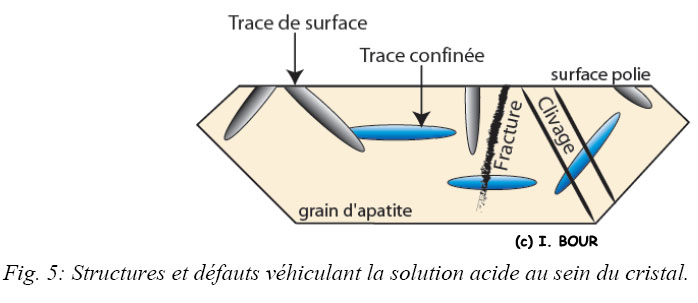
La révélation des traces de fission est effectuée pour des traces recoupant une surface interne du minéral préalablement obtenue par le polissage de la face du plot de résine contentant les cristaux. Seuls les traces et les défauts (microfractures, clivages) interceptant le plan de polissage sont atteints par l’acide (Fig. 5). Par conséquent, c’est généralement les traces de surface qui sont rendues visibles par la révélation acide. Dans certains cas, les traces de fission dites confinées, c'est-à-dire se trouvant plus profondément dans le cristal, peuvent être révélées par l’intermédiaire des autres traces de surface et/ou par des défauts (Fig. 5) qui permettent de véhiculer l’agent acide. Par définition, une trace confinée correspond à une trace totalement incluse dans le minéral et qui ne pourra être révélée que si elle recoupe un ou plusieurs autres défauts du cristal, séquent au plan d’attaque.

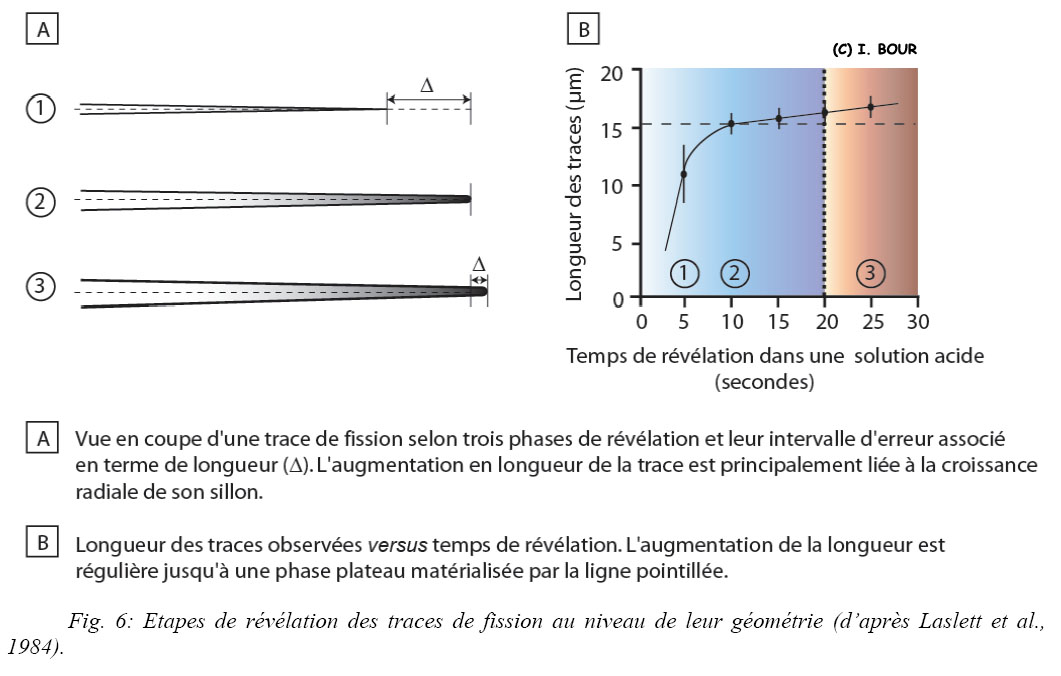
L’attaque acide est réalisée dans une solution d’acide nitrique avec une concentration de 5M à une température de 20±0,5°C durant 20 ± 1s (Tab. 1). La durée du bain acide des échantillons est un paramètre important dans la qualité de révélation des traces de fission (Laslett et al., 1984 ; Fig. 6).

Tab. 1 : Conditions de révélation des traces spontanées dans les apatites.

Lors de l’attaque acide, le diamètre du trou d’attaque , la longueur des traces ainsi que leur densité augmentent de manière progressive et rapide jusqu’à un seuil d’attaque (phase de plateau : Fig. 6). Le protocole d’attaque acide calé sur une durée de 20 secondes est choisi car il correspond au seuil d’attaque (Fig. 6). Les conditions de révélation doivent demeurer identiques pour chaque préparation afin de ne pas introduire un biais sur les longueurs de traces qui seront par la suite mesurées.

La morphologie des traces révélées résulte du rapport entre la vitesse de dissolution de la matière minérale seine Vg et la vitesse de dissolution des traces latentes Vt (Fleischer et Price, 1963a, b). Le rapport des vitesses d'attaque Vg/Vt est toujours inférieur à 1 et caractérise la forme de la trace.

Dans le cas des apatites, la vitesse de dissolution dépend également de l’orientation de la trace par rapport à l’axe cristallographique c. En effet, lors de l’attaque chimique, les vitesses de dissolution Vg et Vt ne sont pas identiques selon les axes du cristal (Masumoto, 1992). Chaque plan cristallographique possède par conséquent son propre taux d’attaque (Fleischer et al., 1975). Ce phénomène peut être assimilé à un ellipsoïde de dissolution propre au système cristallin du cristal (Fig. 7). Dans le plan perpendiculaire à l’axe c, les traces révélées apparaissent sous la forme d’un V et présentent un angle d’ouverture important. En revanche, les traces parallèles à l’axe c apparaissent beaucoup plus fines mais d’une longueur plus importante (Fig. 7). Cette géométrie des traces vient du fait que leur vitesse de dissolution est plus rapide parallèlement à l’axe c. Cela est la conséquence que Vt est plus important parallèlement à l’axe c que perpendiculairement à ce même axe. L’effet de l’orientation cristallographique est à l’origine des différentes géométries de traces en hexagone, en aiguille ou encore en lame de couteau.

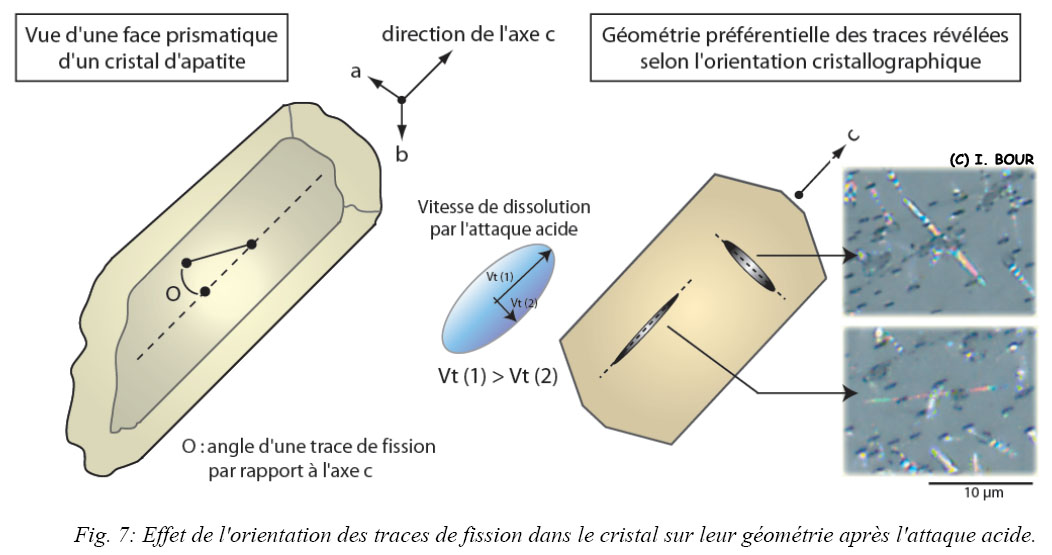
II.1.3.2. Révélation des traces de fission induites

Suite à l’étape d’irradiation, les feuilles de mica (muscovite) sont séparées des échantillons et sont soumises à une attaque par une solution d’acide fluorhydrique (HF) afin de révéler les traces induites. Les feuilles de mica sont attaquées par un bain d’HF à 40 % dans des béchers en Téflon. Les conditions de révélation des traces induites sur micas utilisées dans cette étude sont d’une durée d’attaque de 20±1 minutes à une température de 20±1°C (Green, 1985).
Les feuilles de mica sont rincées dans deux bains successifs d’eau distillée pendant une vingtaine de minutes puis immergées dans un bain d’eau distillée pendant une nuit. Les micas sont par la suite séchés sur une plaque chauffante à 60°C.

II.1.3.3. Reconnaissance d’une trace de fission

L’observation des traces de fission est réalisée à partir d’un microscope optique de type métallographique qui permet de visualiser l’échantillon en lumière transmise (par transparence) et réfléchie (par réflexion). Comme pour la révélation acide, l’emploi d’un protocole de comptage et de mesure des traces est nécessaire et jouera un rôle non négligeable sur la qualité des données. Son application stricte aura pour effet de garder une certaine constance dans la mesure et la comptabilisation des traces. Dans ce protocole, les critères de reconnaissance d’une trace de fission jouent un rôle important.

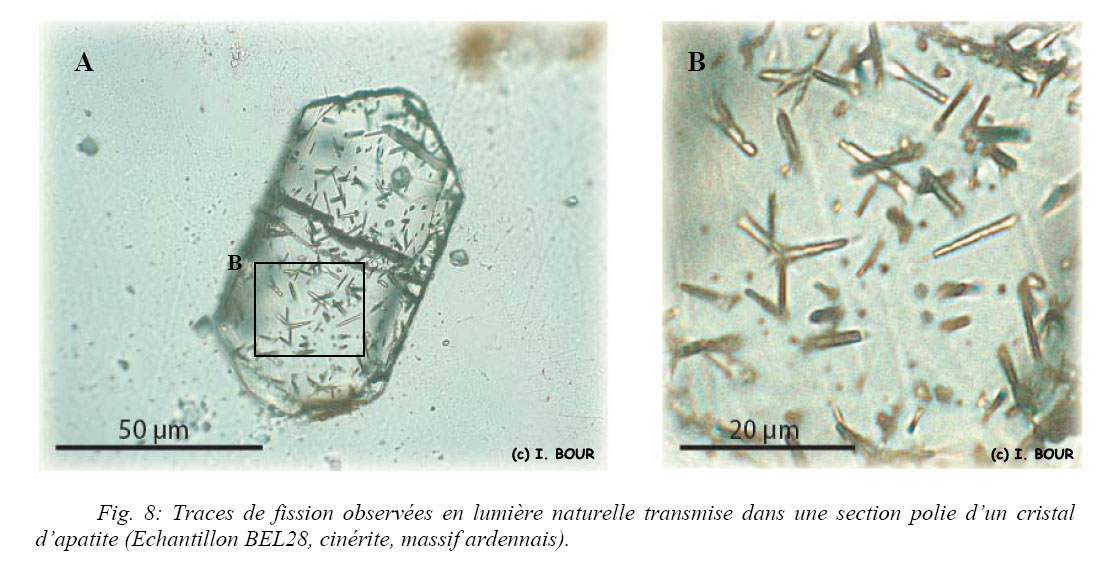
Les traces de fission apparaissent au microscope optique comme des défauts linéaires de longueur finie (inférieure à 20 µm) sans orientation préférentielle (Fig. 8) contrairement aux clivages ou aux dislocations du cristal (Fleischer et al., 1975).
Les traces de fission spontanées recoupant le plan de polissage (traces de surface) se reconnaissent en lumière transmise sous la forme de fins tirets noirâtres (Fig. 8 et Fig. 9(3)) présentant une terminaison en « pointe de flèche ». Selon leur angle d’intersection avec le plan de polissage, les traces spontanées peuvent également apparaître sous l’aspect d’ellipsoïdes. Ces ellipsoïdes correspondent aux trous d’attaque (etch pit) qui sont les points d’entrée de l’acide dans le cristal permettant la révélation des traces latentes. Le diamètre du grand axe de chaque « etch pit » est orienté parallèlement à l’axe c ainsi qu’aux bordures du cristal et correspond aux Dpar selon la définition donnée par Donelick, 1993 ; Burtner et al., 1994 et Carlson et al., 1999 (Fig. 9 (2) et Fig. 10). Cette orientation non aléatoire des Dpar permet de les distinguer de quelconques artefacts. Ce sont les traces de surface qui vont être employées pour la détermination de l’âge TF.

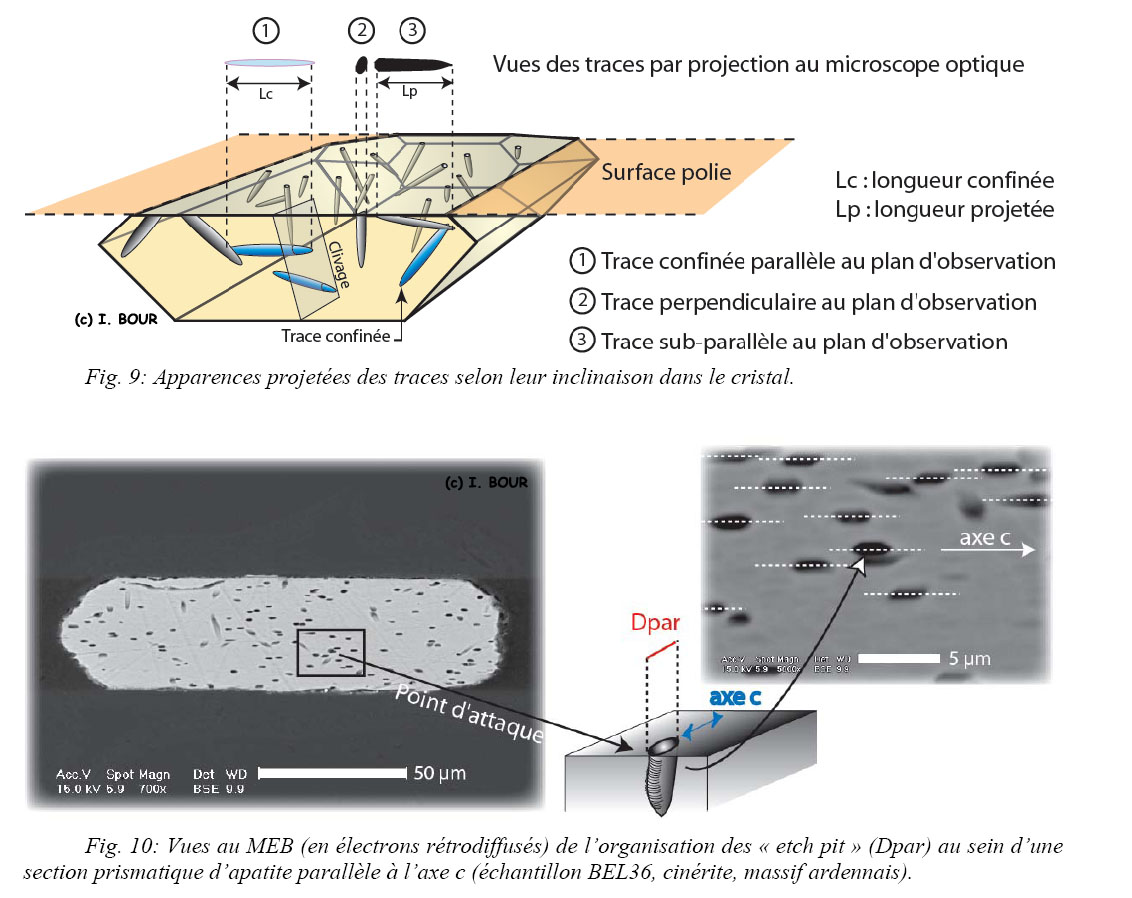
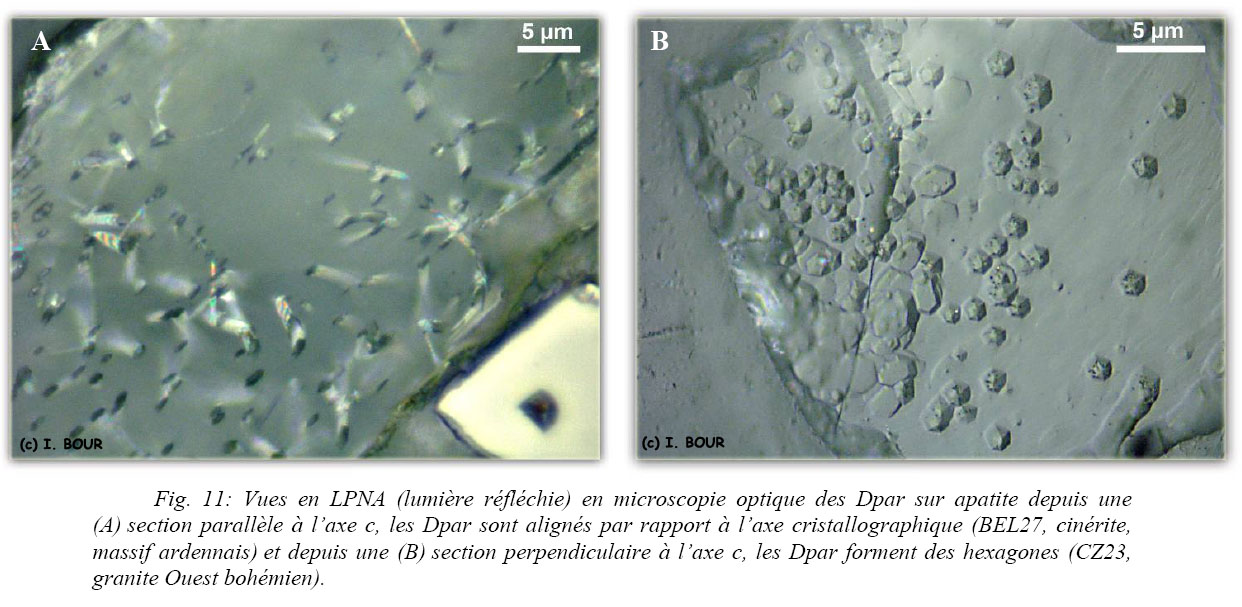
La géométrie en ellipsoïde des points d’attaque (etch pit) générés par l’acide est dépendante de l’orientation cristallographique (Fig. 11A, B). La vitesse d’attaque par l’acide évolue suivant les directions cristallographiques de la même manière que pour les traces. Le point d’attaque présente une géométrie hexagonale (Fig. 11B) et son diamètre est amplifié si le plan d’observation est perpendiculaire à l’axe c. La géométrie du point d’attaque, sous cette orientation, illustre le système cristallin hexagonal de l’apatite.

Les traces confinées se trouvant plus profondément dans le cristal se distinguent en lumière réfléchie et apparaissent sous l’aspect de fins tirets blanchâtres et translucides (Fig. 9 (1) et Fig. 12). Ce sont des traces entières terminées par deux extrémités coniques.

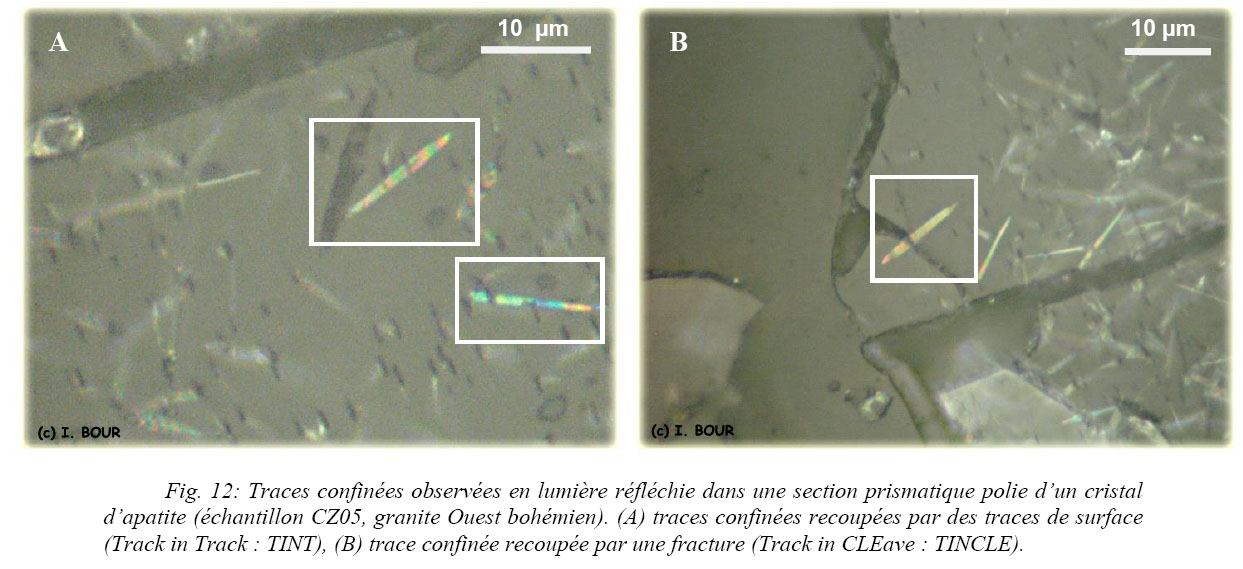
Les traces confinées qui sont disposées parallèlement au plan d’observation sont prises en compte afin de mesurer des longueurs réelles et éviter d’introduire des corrections d’angles qui vont accroître la marge d’erreur dans la mesure. Les mesures de longueur de ces traces confinées sont utilisées pour la reconstitution de l’histoire thermique. Les traces confinées existent sous deux catégories. Elles peuvent être recoupées soit part une autre trace séquente à la surface d’observation (Track IN Track : TINT, Fig. 12A) soit par une fracture ou un clivage également séquent à cette surface (Track IN CLEave : TINCLE, Fig. 12B) (Lal et al., 1969). Dans cette étude, la mesure des TINCLE n’est pas prise en compte. La longueur initiale d’une trace confinée est susceptible de varier notamment dans le cas des tracks in cleavage. Plusieurs théories d’ordres chimiques et microtectoniques existent à ce sujet (Jonckheere et al., 1993). Les fractures drainent des fluides naturels acides pouvant avoir un effet de préattaque chimique sur les traces qu’elles peuvent recouper. La longueur originelle des traces de fission peut donc être altérée. Cette même conséquence peut également être provoquée par un effet extensif de part et d’autre de la fracture.

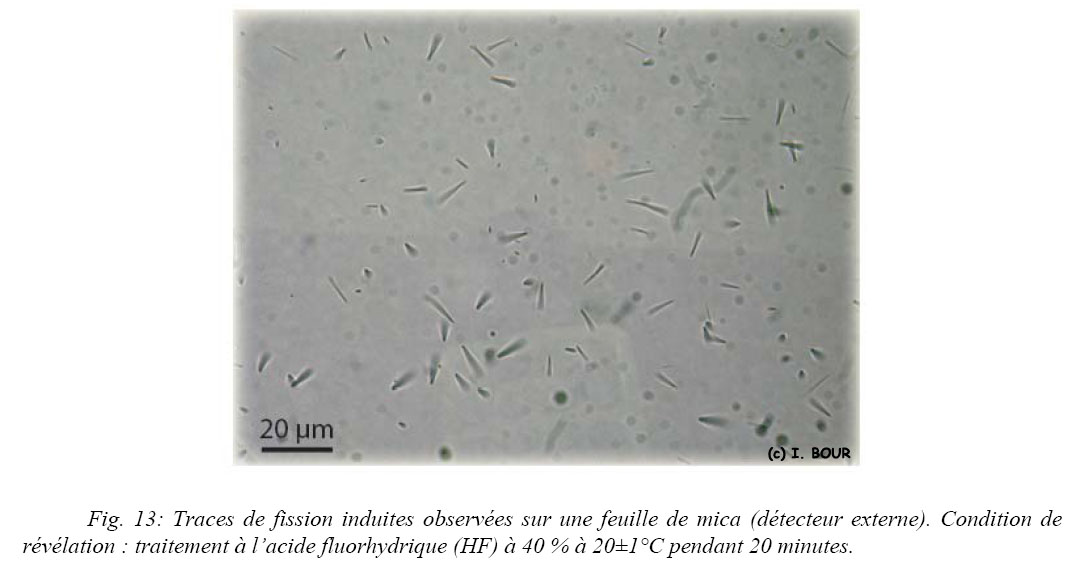
Au niveau des feuilles de muscovite, les traces de fission induites présentent globalement les mêmes caractéristiques de reconnaissance que les traces spontanées observées sur les cristaux d’apatite. Elles apparaissent également sous la forme de fins tirets noirâtres avec une terminaison en pointe et sont dispersées aléatoirement (Fig. 13), en revanche les trous d’attaque sont en forme de diamant (diamond shape) et dépendent du contact entre le détecteur et l’échantillon. Les traces induites sur détecteur externe sont uniquement des traces de surface car elles sont le résultat de la réception de fragment de fission provenant des grains d’apatite sous-jacents.

II.1.3.4. Comptage et mesure

Le comptage des traces de surface et la mesure des longueurs des traces confinées sont réalisés avec un microscope optique métallographique de type Leica DMLM (Fig. 14).

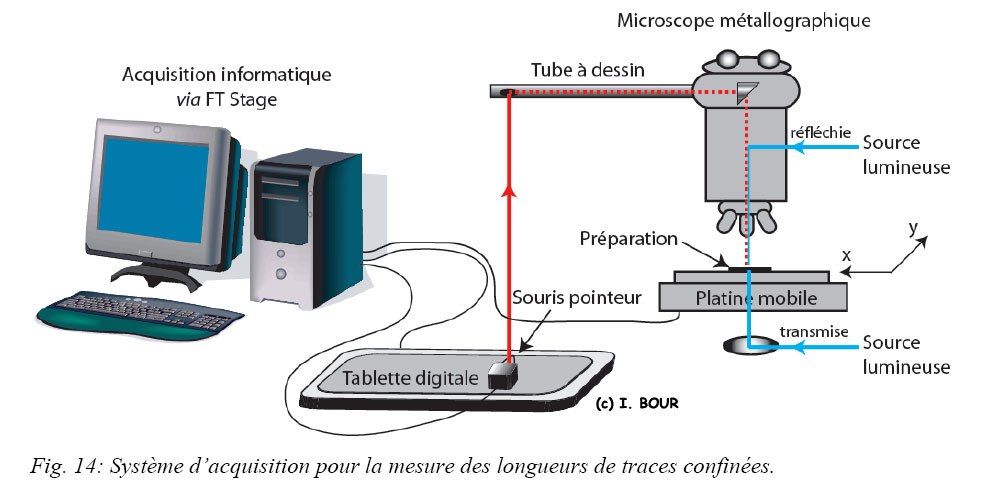
Le microscope est équipé d’une surplatine motorisée (Kinetek) pilotée par le programme de gestion FT Stage (par T. Dumitru). La platine permet d’enregistrer la position de chaque cristal analysé présent dans l’échantillon. Par ce procédé, le programme de gestion peut trouver de manière automatique l’image de ces cristaux au niveau des détecteurs externes (Fig. 15) et passer de l’un à l’autre avec une précision de l’ordre de la dizaine de microns. Cette semi-automatisation permet de gagner en rapidité lors des mesures et limite les erreurs de positionnement notamment lorsque le nombre de traces induites sur le détecteur est faible rendant par conséquent une reconnaissance difficile.

Le comptage est effectué dans une aire définie du cristal, dépourvue d’artefact (cassure, rayure) et d’inclusion minérale pour éviter de quelconques défauts (microfractures) et de possibles variations chimiques (zonation chimique). En effet, la zonation chimique et les inclusions peuvent provoquer un contraste important de la densité des traces (Fig. 16). Il est également préférable de ne pas effectuer de comptage en bordure du grain ainsi que la surface équivalente sur le mica car il existe des problèmes de contact entre l’échantillon et le détecteur externe.

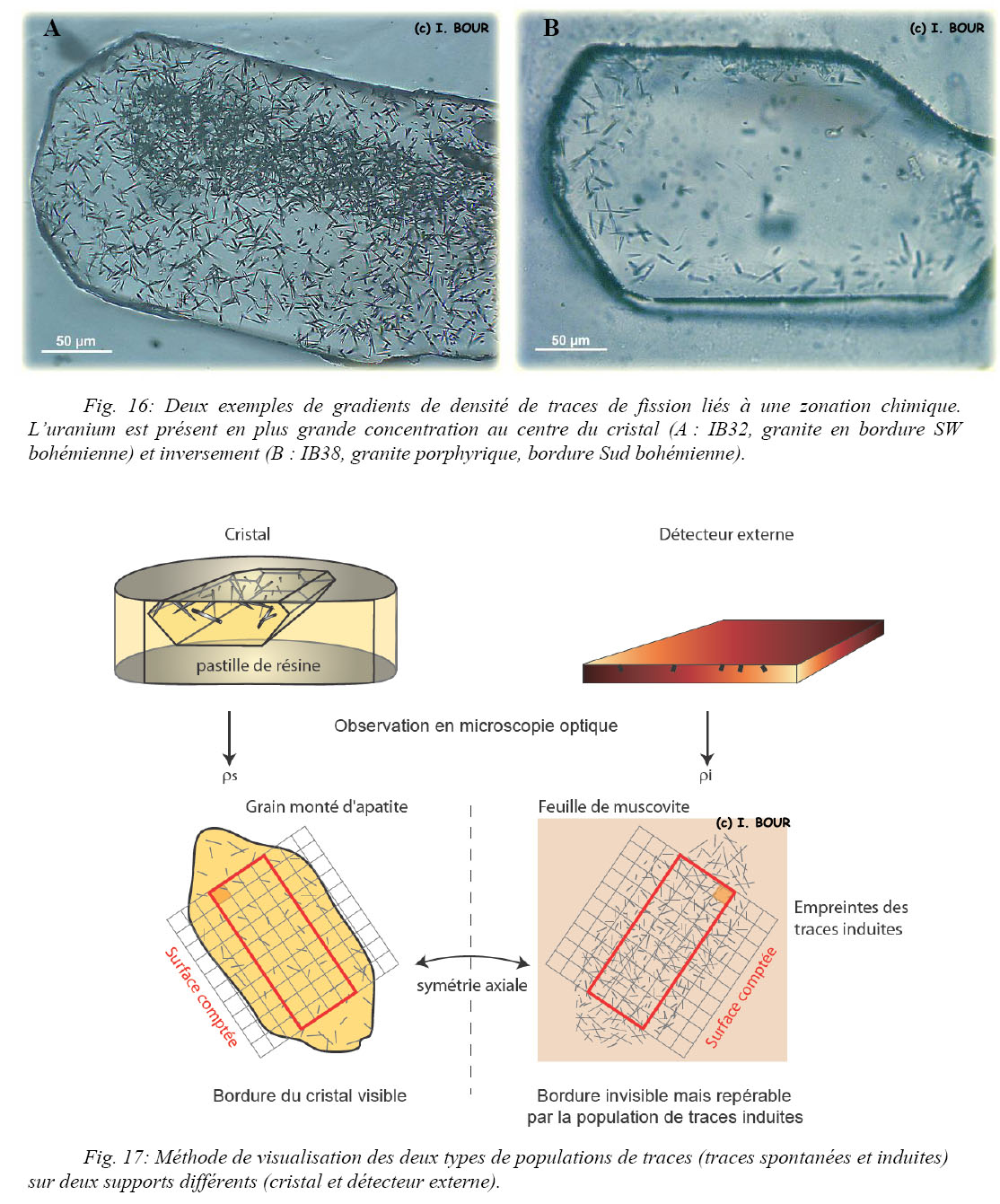
Le comptage des traces révélées (Ns sur le cristal et Ni sur le détecteur) s’opère à partir d’une surface quadrillée issue d’une grille-réticule placée dans un des deux oculaires, ce qui permet de mesurer l’aire de comptage et de déterminer les densités des traces spontanées (ρs) et induites (ρi). Le comptage s’effectue alternativement entre les grains d’apatite et le détecteur (Fig. 17). La surface de comptage et la position du comptage sont identiques entre les deux supports. Le champ d’observation pour la comptabilisation des traces est parcouru par une grille (Fig. 17) composée par des carreaux faisant 10 µm de côté pour un grossissement de 1000 x. Le repère quadrillé va permettre d’organiser le comptage.
La densité de traces est déterminée en rapportant le nombre de traces comptées à la surface de comptage (nombre de cases de la grille réticulée dans lesquelles les traces ont été comptées). La densité des traces (ρs et ρi) est exprimée en nombre de traces/cm² avec ρ(s,i) = N(s,i)/(Ng x S). Ng étant le nombre de cases de la grille dans lesquelles sont comptées les traces et S l’unité de surface égale à 1.10-6 cm².

La mesure des longueurs de traces confinées est effectuée avec le même microscope. La mesure est assistée grâce à une tablette à dessin (digitaliseur Calcomp) et d’une souris curseur munie d’un pointeur électroluminescent de forte intensité visible depuis le microscope (Fig. 14) via un système de renvoi par prisme (tube à dessin). Ce pointeur constitue le repère lumineux entre la tablette digitale et l’échantillon examiné au microscope. En effet, l’image du curseur se surimpose à celle des traces observées. Les traces sont mesurées en pointant les deux extrémités de chacune d’entre elles avec le curseur lumineux. La tablette digitale détermine les coordonnées XY respectives de chaque terminaison de traces. Les paires de coordonnées ainsi obtenues sont listées et stockées dans un tableur sous FT Stage s’occupant d’effectuer automatiquement la conversion des coordonnées en longueur (µm).
Il est préalablement indispensable de vérifier la reproductibilité des mesures avant leur prise en compte. Pour cela, un facteur de calibration de la tablette est déterminé à partir de 50 mesures de longueur sur une même trace. L’erreur systématique sur la mesure d’une trace confinée, dépendant de la précision de visée d’un point ou d’un segment (extrémités des traces confinées), est de l’ordre de 0,2 µm.

Toutes les mesures de longueur des traces confinées et des Dpar s’effectuent sur la face prismatique du cristal reconnaissable par l’orientation commune des Dpar (Fig. 18 A). Les etch pit présentant une orientation désorganisée indiquent que le plan d’observation n’est pas parallèle à l’axe c du cristal (Fig. 18 B). Dans cette situation, les mesures de longueur ne sont pas utilisables.

Le Dpar, correspondant à la moyenne arithmétique du diamètre des traces projetées, est mesuré parallèlement à l’axe c (Fig. 10) de l’apatite (Carlson et al., 1999). Etant de forme ellipsoïdale, les Dpar sont mesurés uniquement au niveau de leur axe majeur. Cinq mesures de Dpar sont réalisées pour chaque grain afin d’établir une moyenne. L’intérêt de prendre en compte la mesure du Dpar permet d’apporter une estimation de la chimie du cristal (estimation de la proportion en chlore notamment) et d’un possible biais de cette chimie sur les valeurs mesurées.

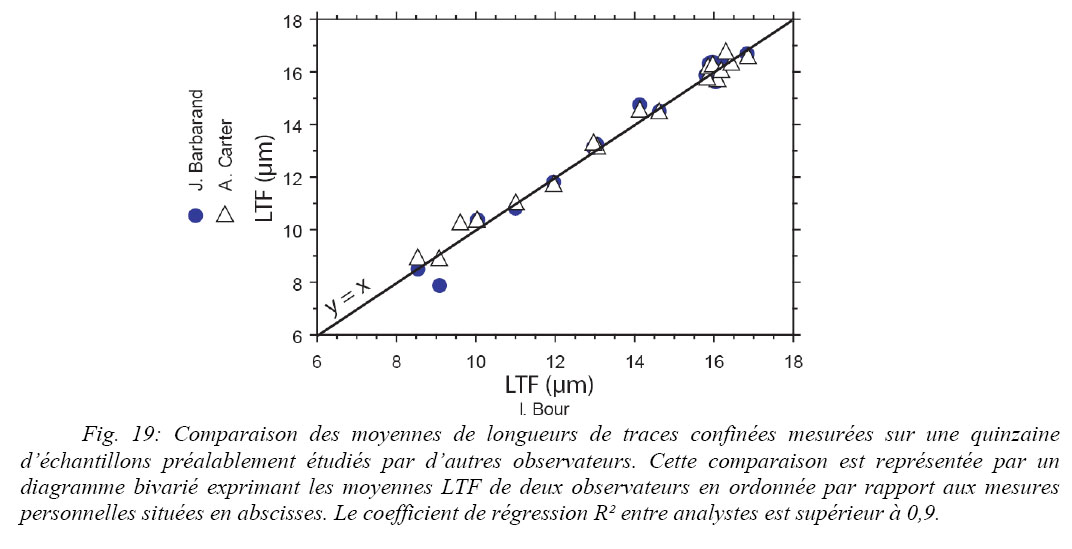
Selon la densité des traces, une centaine de mesures de longueur de trace confinée sont réalisées par échantillon. Il existe quelques méthodes de comparaisons des mesures de longueur de traces entre les analystes mais il n’existe pas de facteur de correction adopté par tous les laboratoires. La seule méthode de normalisation pouvant être utilisée est l’angle des traces par rapport à l’axe c du cristal. A défaut d’un paramètre de correction interlaboratoire, la reproductibilité des mesures de longueur des traces confinées est réalisée sur une quinzaine d’échantillons témoins (apatites de Durango) puis comparée (Fig. 19) entre différents observateurs. Afin de tester la reproductibilité de la concordance des mesures de manière robuste, les mesures sont réalisées sur des séries d’échantillons caractérisés pas des gammes de longueurs de traces variées.

II.1.4. Calcul de l’âge moyen trace de fission

La datation par traces de fission correspondant à un processus de désintégration nucléaire suit, comme d’autres méthodes isotopiques, la loi de décroissance radioactive. Le nombre d’isotopes "père" décroît selon une loi exponentielle avec le temps. Le taux de désintégration dN/dt d’un isotope est proportionnel au nombre d’atomes N présent à un temps t.

Le principe correspond à la loi de décroissance radioactive (1) avec néanmoins quelques adaptations (2).

Dans la méthode de datation par trace de fission, le nombre d’atome fils correspond au nombre de traces accumulées dans un cristal. Corrélativement, le nombre de traces latentes s’accumulant dans un cristal augmente au cours du temps.

La décroissance de l’238U ne se réalise pas par le seul processus de fission spontanée mais également par décroissance α. La constante de décroissance totale (λ) peut être approchée par la constante de décroissance α (λα). Ainsi, la correction du nombre de traces permettant de prendre en compte ce phénomène s’effectue à partir du rapport λf/ λ où λf correspond à la constante de fission. La valeur de λ peut être approchée avec λα avec λ = λf  + λα = λα avec λf  variant entre de 7,03 à 8,46.10-17 an-1 (Bigazzi, 1981). λf est inférieur d’un facteur 106 par rapport à λα dont la valeur est égale à 1,55.10-10 an-1 (Steiger et Jäger, 1977).

La densité de traces ρs, correspondant au nombre de traces spontanées par cm² (déterminée sur surface interne du cristal polie et traitée chimiquement) est fonction du temps et de la teneur en 238U.

Etablir la densité de traces spontanées (ρs) n’est toutefois pas suffisante pour déterminer l’âge trace de fission d’un minéral. Un autre paramètre de concentration est nécessaire : celui de l’238U (élément père) ou un paramètre qui en dépend. Le rapport des abondances isotopiques 235U/238U est une constante connue. Il est donc possible de déterminer la teneur en 238U si l’on est capable de mesurer celle de l’235U.
La détermination de la concentration en 235U s’opère en provoquant sa fission induite, c'est-à-dire artificiellement grâce à un réacteur nucléaire. La fission induite des atomes d’235U est déclenchée par capture neutronique grâce à une irradiation générant un flux de neutrons thermiques faiblement énergétique (< à 0,2 MeV). Les échantillons ont été irradiés dans le canal P1 du réacteur ORPHEE au CEA de Saclay (Commissariat à l’Energie Atomique, laboratoire Pierre Süe). Les caractéristiques du canal P1 ont été décrites par Meyer (1990). La fluence demandée est de 4,9.1015 neutrons/cm2 soit 6 minutes d’irradiation pour un flux nominal estimé de 1,37.1013 neutrons/cm2/s.

La densité de traces induites (ρi) ainsi générées dans un minéral irradié est dépendante de la concentration en 235U et de la fluence Φ utilisée. La constante de désintégration par fission spontanée de 238U (λ238U) étant supposée connue, ce système peut, dans ce cas, jouer le rôle de géochronomètre en tenant compte de la composition isotopique I = 235U/238U de l'uranium qui est constante dans l’actuel.

Le comptage est ainsi effectué sur deux types de support d’où l’introduction d’un facteur géométrique g. Le facteur g correspond au rapport entre la géométrie de type 4π stéradians pour une observation réalisée dans un volume cristallin (l’échantillon) et 2π stéradians pour une observation réalisée sur un détecteur externe. Sur ce dernier, l’observation s’effectue sur une surface (g = gi/gs) où g est une valeur purement théorique.
D’après Gleadow et Lovering (1977), le fait de travailler sur des cristaux d’apatite dont les faces sont parallèles à l’axe cristallographique c avec un détecteur externe en muscovite, permet d’obtenir la constance du paramètre g approchant la valeur de 0,5.

A partir de ces conditions, l’équation d’âge par traces de fission (3) peut se présenter sous cette forme,

La dosimétrie neutronique est assurée par des pastilles de verre (dosimètre), ou "moniteurs", contenant une concentration connue en uranium. Ces dosimètres sont irradiés conjointement aux cristaux à dater et sont utiles pour caractériser la fluence neutronique. Leur irradiation provoque la fission de l’235U par capture neutronique. La fluence est déterminée, après irradiation, par comptage des traces de fission induites produites dans le moniteur.

Les neutrons interagissent avec les échantillons  En effet, le flux entrant de neutrons sera différent du flux sortant et variable d’une session d’irradiation à une autre (Tab.2). La détermination de ce flux en différents points équidistants va être donnée par la densité moyenne des traces induites « imprimées » sur le détecteur externe des dosimètres (ρverre). Les densités moyennes de traces issues des trois dosimètres seront utilisées pour le calcul du facteur zêta décrit plus en aval.

 Tab. 2: Pourcentages de fluctuation du flux neutronique à travers les montages comparés entre plusieurs séquences d’irradiations. Le flux est variable d’une séance d’irradiation à l’autre et selon le montage du conteneur.

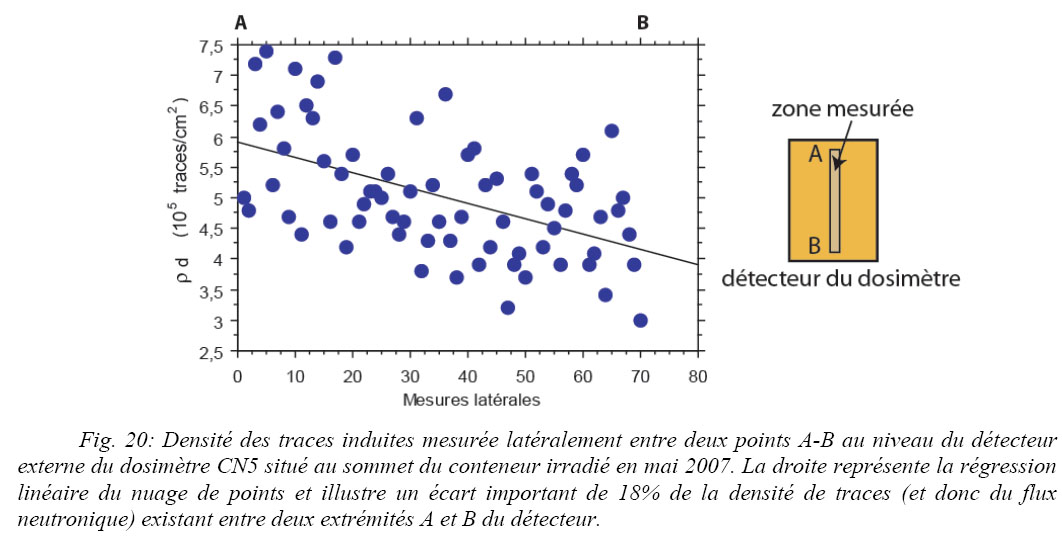
Il apparaît que le flux de neutrons ne présente pas d’évolution régulière du haut vers le bas du conteneur. Il est donc possible que des variations intermédiaires entre deux dosimètres aient lieu. Les variations latérales du flux neutroniques sont plus importantes par rapport aux variations verticales (Fig. 20). Il existe un gradient pouvant être supérieur à l’écart existant entre les trois dosimètres (selon la position du dosimètre dans le conteneur).

La densité de traces induites, enregistrée par les détecteurs externes associés aux pastilles de verre (ρd), est proportionnelle à la fluence Φ, c'est-à-dire :

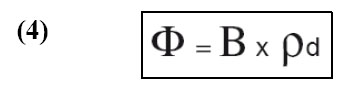
B est une constante caractéristique du dosimètre en relation avec le flux neutronique (facteur de proportionnalité). Il exprime le rapport entre les neutrons et les traces induites. En combinant les expressions (3) et (4), l’équation d’âge devient ainsi :

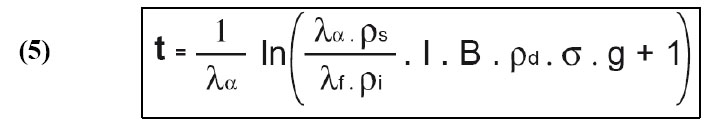
Néanmoins, l’équation d’âge sous cette forme pose problème. En effet, la détermination du paramètre B et donc la fluence neutronique Φ (4) est très délicate à obtenir et réclame une expérimentation lourde (De Corte et al., 1991 ; Van den Haute et al., 1988). La valeur du λf n’est connue qu’à environ 15 %. L’utilisation d’une forme différente de l’équation d’âge et l’introduction d’un nouveau paramètre de substitution zêta (ζ) permettent de contourner cette complication (6).

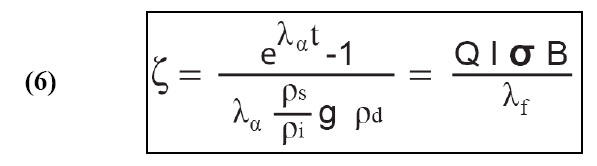
La méthode du zêta (Hurford et Green, 1983) permet d’intégrer les termes difficiles à déterminer dans un seul facteur.  ζ est un paramètre déterminé de manière expérimentale par calibration à partir de standards (échantillons d’âge connu). La valeur ζ doit être déterminée par chaque observateur (Hurford, 1990). Cette valeur dépend des conditions de révélation et d'observation des traces (façon de compter les traces de fission au microscope représentée par le paramètre Q : facteur d’observation). ζ varie également selon le verre moniteur utilisé (dosimètre) et les laboratoires (thermalisation des neutrons du réacteur, position d’irradiation).

La détermination expérimentale du facteur ζ est réalisée à partir de plusieurs échantillons de cristaux d’apatite reconnus internationalement en terme de standard et dont l’âge est parfaitement connue par le biais de plusieurs méthodes de datation absolue (K/Ar et 40Ar/39Ar). La détermination du facteur ζ est réalisée conformément aux recommandations de l’I.U.G.S. (Hurford, 1990) spécifiant au minimum l’utilisation de trois irradiations et deux standards pour obtenir un facteur z moyen valide.

Deux apatites ont été sélectionnées comme standard d’âge par la sous-commission de géochronologie de l’I.U.G.S. (Hurford, 1990) :

Dans nos mesures, les standards de Durango et de Fish Canyon Tuff ont été utilisés pour la détermination du facteur de calibration Zeta (z) appliqué aux cristaux d’apatite.

Le facteur z moyen est obtenu à partir de la moyenne pondérée (7) des différentes valeurs de z  individuels (ZMPS : Zêta Moyen Pondéré Standard ; Green, 1985). L’inverse de l’erreur sur chaque valeur (±1σ) correspond au facteur de pondération.

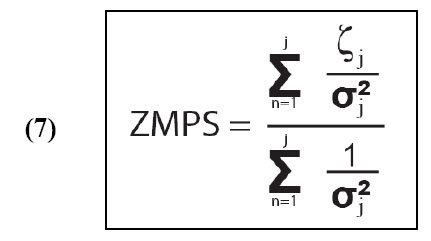
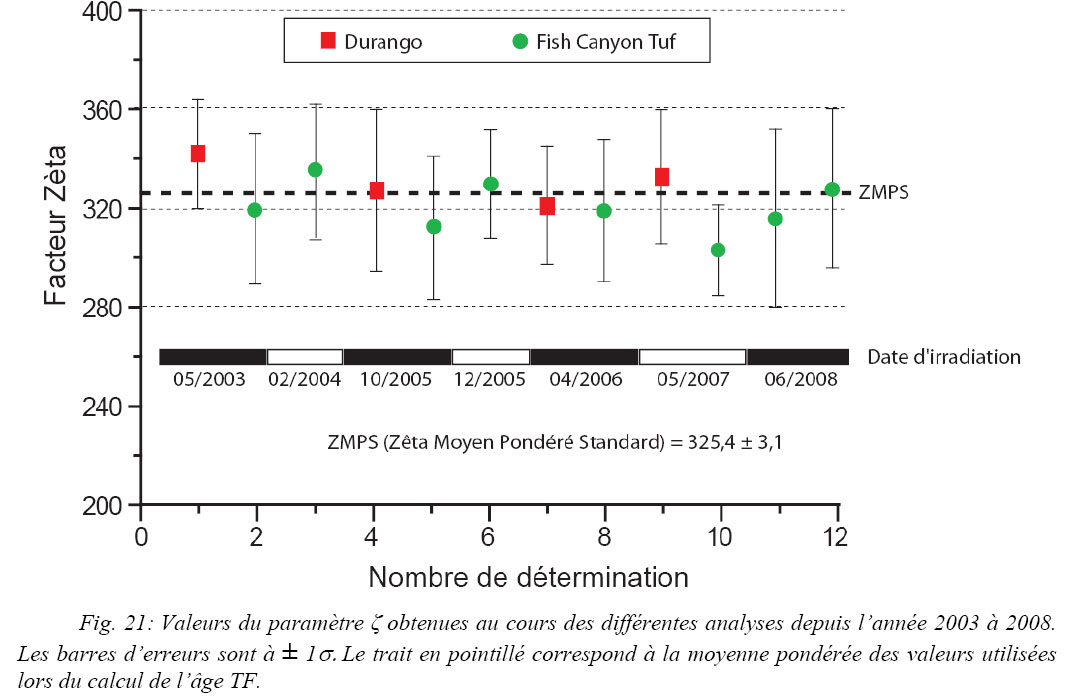
Douze échantillons étalons provenant de huit irradiations différentes avec leurs dosimètres associés ont été mesurés pour déterminer le facteur z  personnel (Tab. 3 ; Fig. 21). Les grilles de mesure pour la détermination du  z  figurent dans l’Annexe 2.

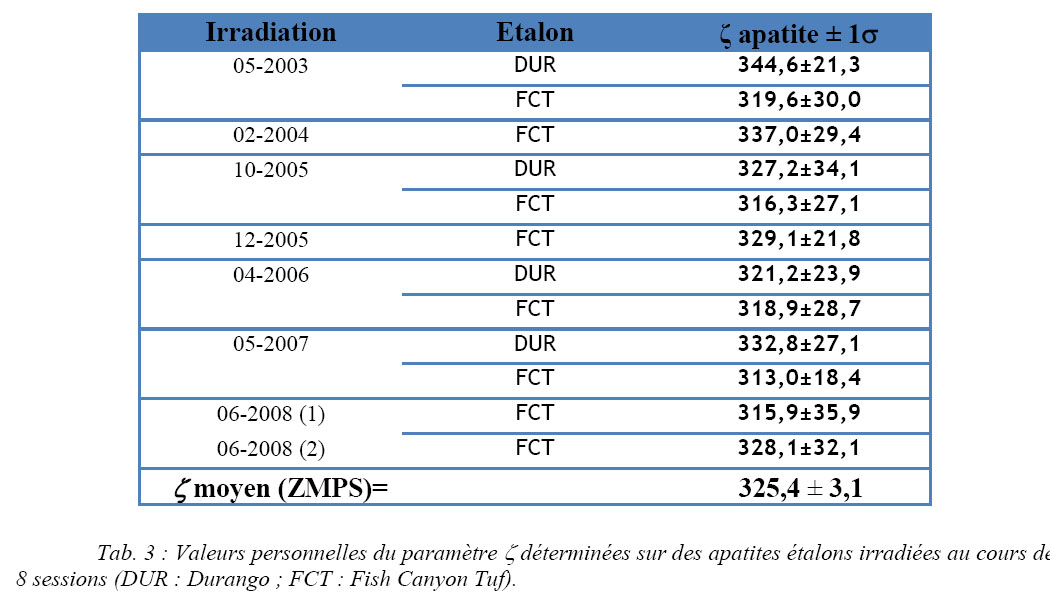
La valeur pondérée personnelle du z  est de 325 ± 3 (avec l’emploi de dosimètres CN5). Les valeurs du z  fluctuent faiblement au cours des mesures dans le temps et des multiples irradiations (Fig. 21). Cette valeur pondérée a été adoptée pour l’ensemble des datations présentées dans ce travail.

L’expression finale de l’équation d’âge utilisée dans ce travail, selon la méthode du détecteur externe, s’écrit telle que :

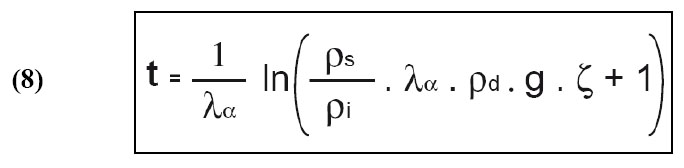
La méthode de l'âge central (Galbraith et Laslett, 1993) a été utilisée pour le calcul de l'âge TF de chaque échantillon. Cette méthode permet de calculer la moyenne de la distribution logarithmique des âges individuels correspondant aux âges des différents grains analysés. Elle permet également de reconnaître la variation des âges et l’existence de plusieurs populations de grains.

II.1.5. Stabilité thermique des traces et significations des âges trace de fission

Les âges TF sont différents (plus récents dans la plupart des cas) que les âges obtenus par d’autres méthodes radiogéniques. Ce « rajeunissement » est lié à l’action de la température. Etant donné que la température augmente avec la profondeur, l’âge apporte ainsi des informations sur l’exhumation des roches c'est-à-dire la détermination du taux moyen de remonter de la roche depuis de faibles profondeurs (< 4000 m) dans le cas d’un système à l’équilibre. L’âge TF représente très rarement l’âge absolu de la roche. Plus l’âge TF d’une roche est ancienne, plus cette roche a subi une phase d’exhumation précoce. L’âge TF d’une roche intègre les événements thermiques subis par cette dernière au cours de son histoire (Wagner, 1981). En complément de l’âge TF, l’analyse statistique de la distribution des longueurs de traces permet de reconstituer, de manière continue, la chronologie d’une histoire thermique linéaire ou polyphasée (Gallagher et al., 1998). L’ensemble des informations géologiques qui est contenu dans ces longueurs de traces n’est pas livré par le seul calcul de l’âge TF décrit plus haut.

Lors de la fission spontanée, les fragments de fission parcourent une certaine distance dans le réseau cristallin. Cette distance de parcours dépend de l’énergie Ec et de l’espèce minérale. Par conséquent, les traces spontanées sont considérées comme ayant une longueur initiale constante de 15±1 µm (Gleadow et al., 1986).

La datation de cristaux d’apatite, prélevés dans des forages pétroliers, a montré que la température (répartie autour d’une valeur) est le principal facteur générant l’instabilité des traces de fission fossiles (Fleischer et al., 1975). Le réseau cristallin désorganisé par le passage des fragments de fission possède la capacité de se réorganiser de manière spontanée et instantanément à l’échelle des temps géologiques sous l’effet de la température (restauration du réseau cristallin par diffusion intracristalline). En effet, à partir d’un seuil de température, le réseau cristallin se réorganise progressivement produisant une diminution de la longueur des traces jusqu’à leur disparition. Ce raccourcissement est dépendant de la durée de résidence dans une gamme de températures donnée. Les traces de fission sont préservées dans la structure cristalline en dessous d’une température seuil. Cette longueur initiale va varier entre 0 et 15 µm en fonction de la température.
La longueur des traces est directement contrôlée par la vitesse de remontée (ou d’enfouissement) de la roche. Cette vitesse est dépendante du temps de résidence de la roche à différents paliers de températures, elle-même reliée à la profondeur d’enfouissement. Il est ainsi possible d’interpréter plus en détail un âge TF, en terme de message géologique, grâce à l’examen de la distribution statistique des longueurs de traces confinées pour chaque échantillon.

II.1.5.1. Zones de stabilité des traces

La vitesse d’effacement des traces dépend de plusieurs paramètres notamment de l’évolution thermique de la roche, mais également de l’axe cristallographique (Laslett et al., 1984) ou encore le rapport Cl/F des apatites (Green et al., 1985).

La longueur des traces varie selon un intervalle de températures. Il est ainsi possible d’introduire le concept de zone dite de rétention partielle des traces de fission (Green et al., 1989 ; Gallagher et al., 1998 ; Fig. 22). Les extrema thermiques de la zone de rétention partielle, compris entre 60 et 110°C, sont bien contraintes pour l’apatite (Gleadow et Duddy, 1981 ; Green et al., 1989). Par conséquent, si un évènement thermique de refroidissement a eu lieu pour des températures inférieures à 110±10°C, il sera possible de reconnaître les traces fossiles enregistrées antérieurement et postérieurement à l’événement grâce à leur longueur. La longueur de la trace peut être réduite par l’augmentation de la température ou la diminution de la vitesse (ou durée) de transit dans la zone de rétention partielle lors d’une exhumation (Carter et Gallagher, 2004).

En partant de la surface, trois domaines de stabilité thermique des traces de fission sont définis pour l’apatite (Fig. 22) (Wagner et Storzer, 1972 ; Gallagher et al., 1998).

• Zone de rétention totale ZST (I). Cette dernière couvre un champ de températures depuis la surface (affleurement) jusqu’à l’isotherme 60°C. A ce niveau, la stabilité du réseau cristallin est grande et permet l’enregistrement et la conservation complète de toutes les traces (Fitzgerald et Gleadow, 1990). Les traces possèdent leur longueur maximale. L’influence de la température en base du domaine sur les traces est toutefois possible mais extrêmement ténue (Carter et Gallagher, 2004).

• Zone de rétention partielle ZRP (II). Le réseau cristallin amorce une réorganisation mais de manière incomplète au niveau des traces. Celles-ci sont encore identifiables (cicatrisation ou recuit partiel). Le réseau cristallin conserve les traces générées mais sont néanmoins raccourcies au cours du temps. Pour les apatites la ZRP se situe entre 60°C et 110°C (Wagner et Van den Haute, 1992). Pour une durée de résidence prolongée dans cette zone, les traces seront d’autant plus courtes. Ce constat est d’autant plus vrai en base de ce domaine.

• Zone de non rétention ZNR (III). C’est une zone d’instabilité totale où la température est supérieure à 110±10°C et correspond à un domaine de comportement élastique du réseau cristallin. Les traces dans cette zone ne sont pas stables et leur durée d’existence est très brève en raison de la réorganisation rapide du réseau cristallin. L’effacement des traces fossiles est complet et correspond au recuit ou à la remise à zéro du chronothermomètre défini par les traces.

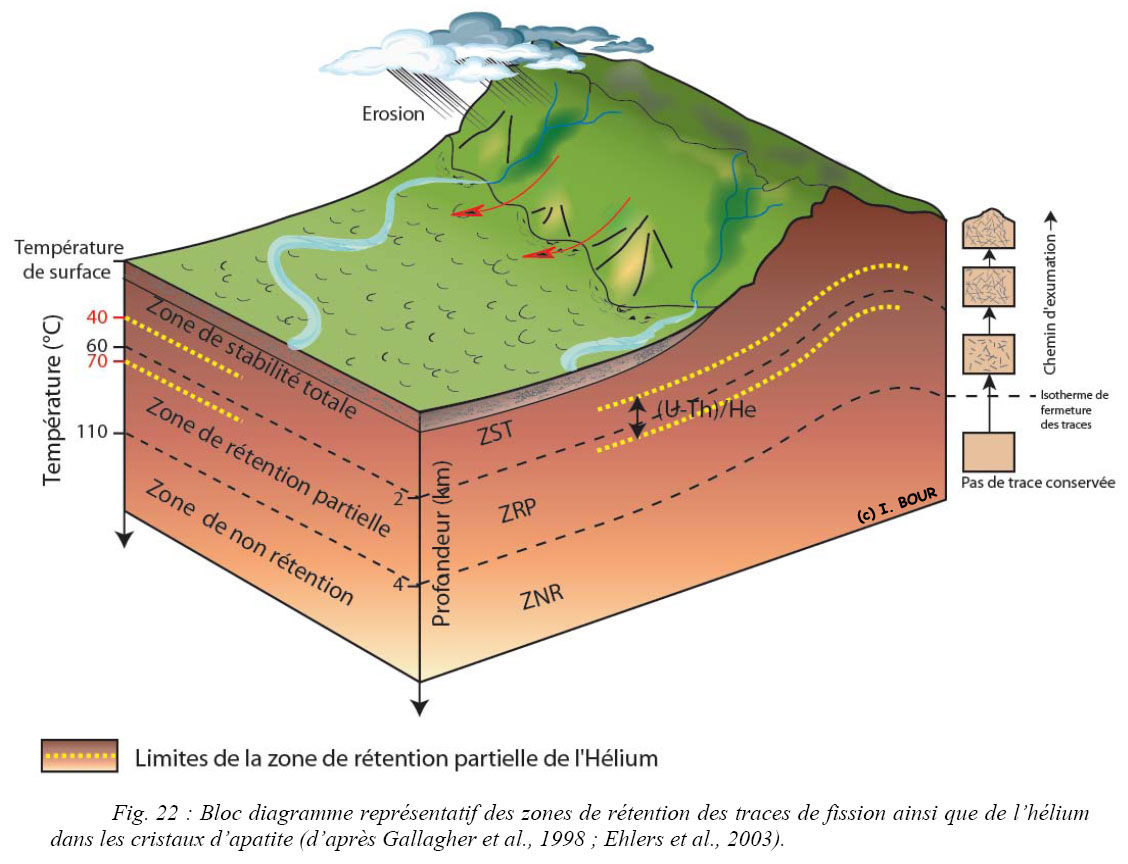
Les températures limites caractérisant les trois zones de stabilité des traces peuvent varier selon le temps de résidence de l’apatite à une température donnée, selon le taux de refroidissement/réchauffement et également selon la nature des cristaux. Le concept de la ZRP est illustré sous sa forme simplifiée (Fig. 22).

II.1.5.2. Distribution et interprétation des longueurs de traces confinées

Les deux paramètres principaux qui contrôlent la cinétique de cicatrisation des traces (dont la longueur est un indicateur de l’histoire thermique) sont la température et le temps.

La cinétique de cicatrisation des traces est anisotrope. Les traces orientées selon un angle élevé ont une cinétique de cicatrisation plus rapide que les traces parallèles à l’axe c. Cette anisotropie augmente avec le degré de cicatrisation des traces (Laslett et al., 1984; Green et al., 1986 ; Donelick et al., 1990; Galbraith et al., 1990 ; Donelick, 1991 et Donelick et al., 1999).Afin de corriger l’influence de l’anisotropie des longueurs de traces présentes dans l’apatite (Carlson et al., 1999), l’angle des traces confinées par rapport à la direction de l’axe c est prise en compte. La normalisation des angles de projection des traces par rapport à l’axe c améliore chaque aspect de la reproductibilité de mesure de longueurs (Ketcham et al., 2006). La normalisation accélère la convergence de la moyenne des longueurs dans des analyses simples, augmente la cohérence (reproductivité) parmi les mesures effectuées par un analyste et augmente également la cohérence des mesures sur des mêmes supports effectuées par des analystes différents. Normalisées, les longueurs des traces augmentent aussi la concordance de la prédiction des histoires géologiques (Ketcham et al., 2006).

L’examen de la distribution des longueurs de traces confinées, couplé avec l’âge apparent du cristal, permet d’interpréter et de modéliser chronologiquement les différents épisodes thermiques que les apatites ont subi au cours de leur histoire depuis le dernier refroidissement en dessous de 110±10°C.
La signification des différentes classes de longueurs des traces observées dans les cristaux d’apatite est comprise depuis une vingtaine d’années (Gleadow et al., 1986). L’écart-type de la longueur des traces augmente avec l’accroissement de la température (Green et al., 1989 ; Green, 1992 ; Gallagher et al., 1998 : Fig. 23). L’évolution des longueurs de traces est un processus non linéaire mais des modèles numériques permettent d’évaluer le chemin temps-température et nous renseigne sur l’histoire thermique des échantillons.

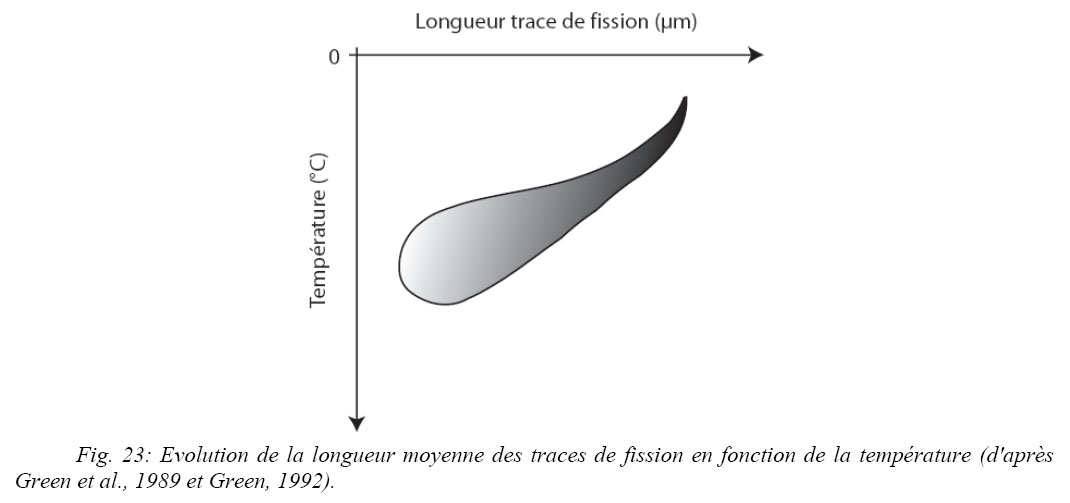
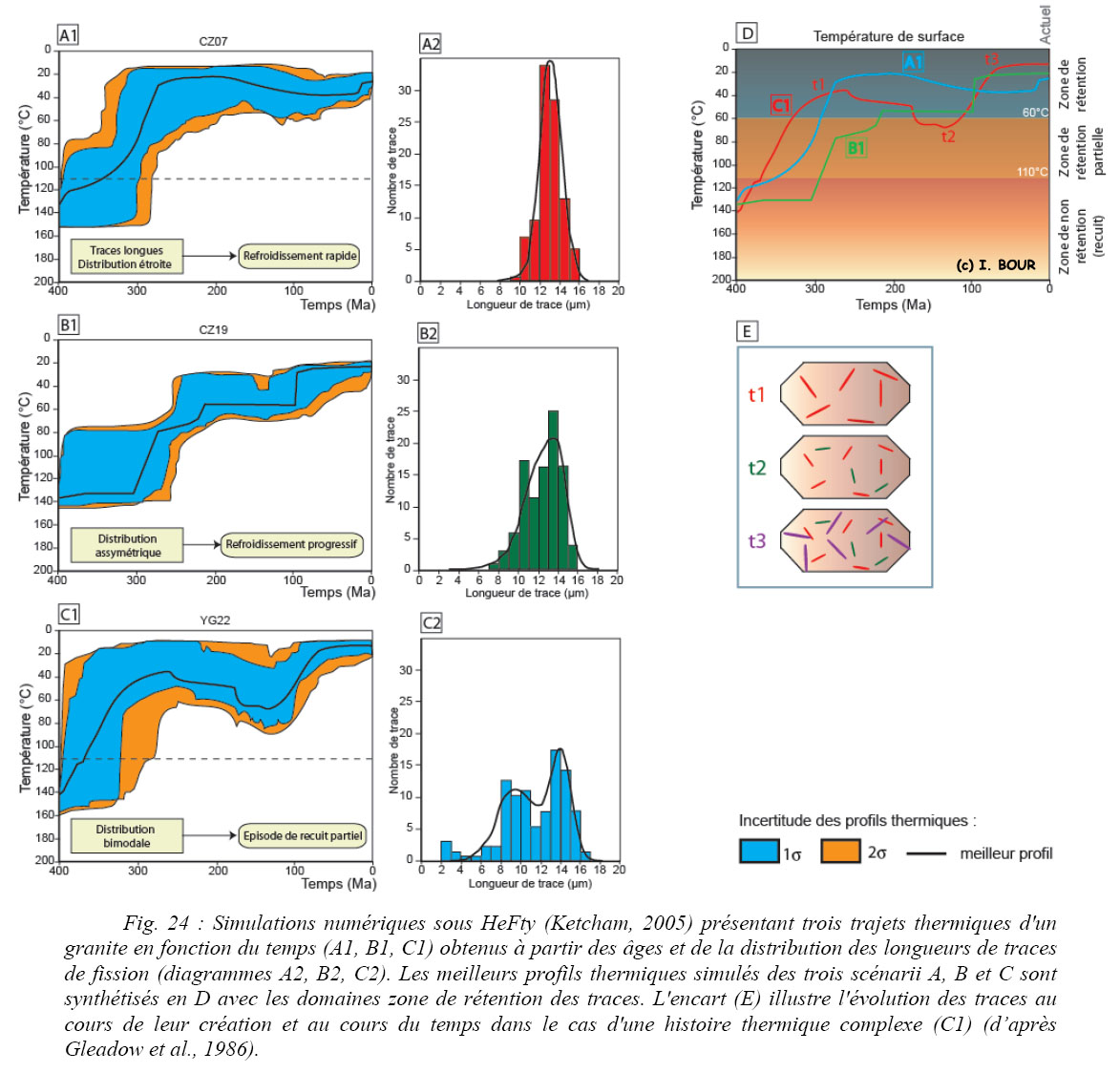
La longueur moyenne et la distribution des traces confinées renseignent sur l’histoire thermique. La distribution des longueurs, matérialisée par des géométries d’histogrammes caractéristiques (gaussienne symétrique, asymétrique, bimodale), permet de définir trois modèles thermiques types (Gleadow et Brown, 2000).

• Le scénario I (Fig. 24A1) exprime le cas de roches qui ont subi un refroidissement très rapide, synonyme d’une exhumation brutale tels que le fonctionnement d’une faille ou une orogenèse. La distribution des longueurs de traces présente un écart-type étroit (≤ à 1 µm) et forme une courbe unimodale. La longueur moyenne est majoritairement comprise entre 13 et 14 µm (Fig. 24A2). Dans cette situation, la grande majorité des traces se forme à une température inférieure à 60°C. Le scénario démontre un temps de résidence très court dans la zone de rétention partielle.

• Le scénario II (Fig. 24B1) démontre le cas d’une diminution progressive de la température induisant un refroidissement linéaire suite à une érosion à taux constant. La dispersion des longueurs de traces évolue entre 5 et 15 µm. L’écart-type est supérieur à 1 µm et peut atteindre 2 µm selon le taux de refroidissement et le temps de résidence (plus long que dans le cas précédent) dans la zone partielle de rétention. La longueur moyenne dominante est de l’ordre de 12 à 13 µm (Fig. 24B2). L’histogramme de distribution des longueurs suit une courbe gaussienne asymétrique aplatie comprenant des longueurs de traces courtes. La forme de cette distribution est liée au fait que les traces de fission se forment en continu et sont partiellement cicatrisées.

• Le scénario III (Fig. 24C1) représente un parcours plus complexe de la roche avec une phase d’enfouissement. Cette évolution discontinue de la température implique une distribution bimodale de la population de traces dont l’écart-type peut atteindre 3 µm et fait ressortir deux pics de longueur de traces calés autour de 9 µm et 15 µm (Fig. 24C2). La distribution des longueurs est caractéristique de deux épisodes de refroidissement et d’une augmentation de la température intermédiaire. L’augmentation de la température  implique le retour des roches dans la zone de rétention partielle et provoque le raccourcissement des traces. Les traces formées après l’événement thermique, c'est-à-dire lors du refroidissement final, sont plus longues (Fig. 24E). Cela implique l’enregistrement de deux populations de longueur de traces au sein du cristal.

Ces trois cas de figures sont des scénarii types. Dans de nombreuses situations, l’obtention des distributions de longueurs de trace n’est pas toujours aussi caractéristique. Il existe de nombreux cas intermédiaires.

II.2. Analyses (U-Th)/He

II.2.1. Introduction

L’utilisation de cette méthode pour des datations radiochronologiques a vu le jour au début du XXème siècle (Strutt, 1903 ; Rutherford, 1906). La méthode (U-Th)/He sur apatite a suscité un regain d’intérêt depuis l’étude de Zeitler et al. (1987). Ils furent les premiers à montrer la faisabilité et l’intérêt de ce thermochronomètre et ont proposé que les datations par l’hélium fournissent des âges de refroidissement correspondant à la fermeture du système minéral pour de très basses températures par rapport aux autres systèmes radiochronologiques classiques utilisés. Les premières expériences de diffusion ont permis d’établir une température de fermeture inférieure à 100°C dans le cas de cristaux d’apatite (Zeitler et al., 1987 ; Lippolt et al., 1994 ; Wolf et al., 1996b).
Les études employant cette méthode ont débuté à partir de 1997 (Reiners et Farley, 1999). Cette dernière permet d’avoir accès à l’histoire thermique à basse température d’un objet géologique donné (chaînes de montagnes, bassins sédimentaires) et donne également accès  aux âges d’exhumation et d’évènements thermiques tout comme les traces de fission.

Le résultat initial était que les âges obtenus par la méthode (U-Th)/He sont plus sensibles aux faibles températures mais, en réalité, les dernières études (Green et al., 2006 ; Flowers et al., 2009 ; Gautheron et al., 2009) proposent une sensibilité thermique très variable et voir même équivalente par rapport aux traces de fission. Ces nouvelles données seront discutées plus en aval.

II.2.2. Principe de la méthode

Dix radionucléides de grande longévité produisant naturellement des particules α existent sur  Terre : 144Nd, 147Sm, 148Sm, 152Gd, 174Hf, 186Os, 190Pt, 232Th, 235U et 238U. Pour la technique de la thermochronologie hélium, tous les radionucléides, à l’exception des trois plus lourds en terme de masse atomique, peuvent être négliger à cause de leur très faible abondance et leur faible productivité en particules alpha. Le thermochronomètre (U-Th)/He est basé sur l’émission et l’accumulation de particules alpha (noyaux d’hélium) dans le minéral lors de la désintégration radioactive de l’238U, 235U et du 232Th contenus dans l’apatite (Rutherford, 1905 ; Zeitler et al., 1987 ; Wolf et al., 1998).

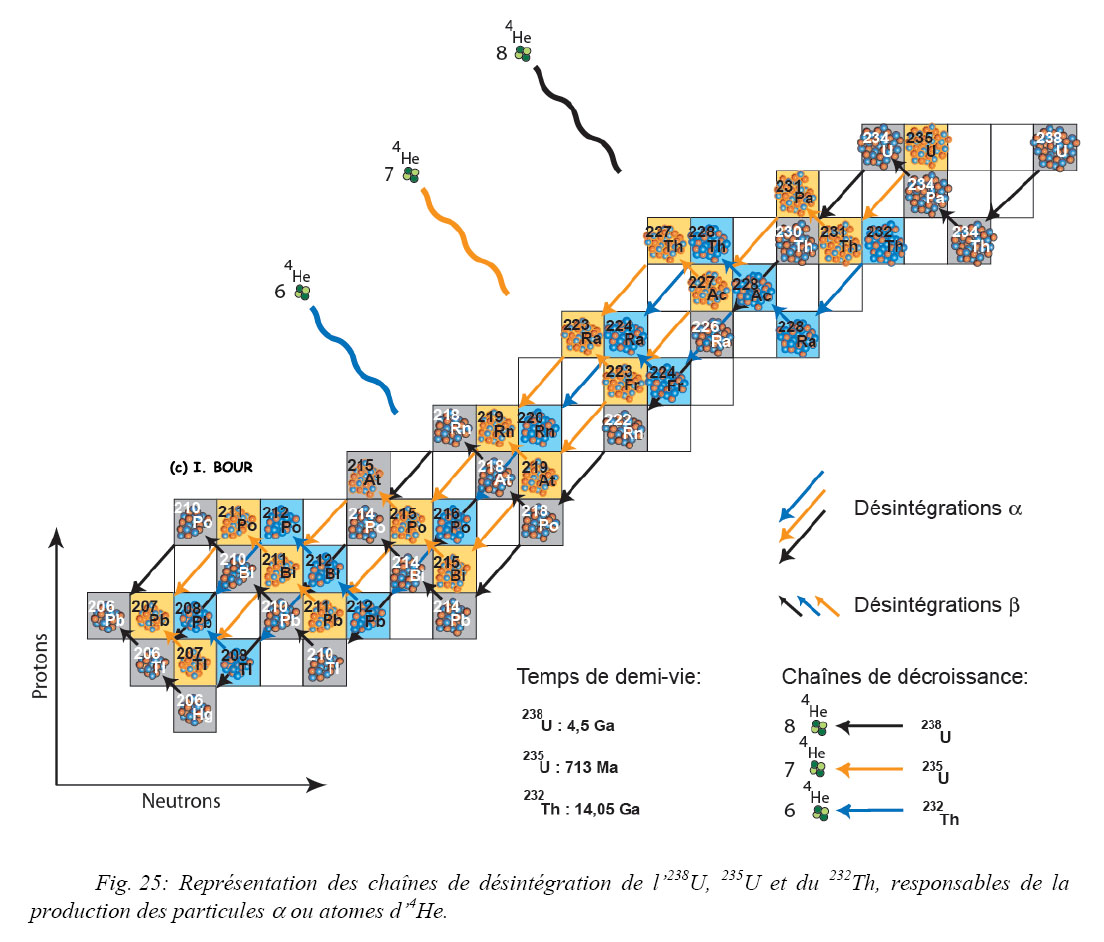
8 noyaux d’hélium sont générés à partir de la désintégration de l’238U (élément père) en un atome plus léger de 206Pb (élément fils). 7 autres noyaux d’hélium sont générés dans la chaîne de l’235U au 207Pb et 6 autres dans la chaîne du 232Th au 208Pb (Fig. 25). La mesure précise des abondances actuelles en 4He, 238U, 235U et 232Th permet d’acquérir un âge correspondant au temps écoulé depuis que l’4He est retenu dans la structure cristalline du minéral hôte et donne ainsi accès à l’âge de fermeture du système, c'est-à-dire à l’âge où la diffusion de l’hélium est négligeable en deçà d’une certaine température.
La diffusion de l’He est ainsi contrôlée par la température et permet d’appréhender l’histoire thermique d’un échantillon. L’âge (U-Th)/He correspond, comme pour les traces de fission à un âge thermique intégrant le chemin temps-température que la roche a subi au cours de son histoire.

Cette technique s’utilise plus facilement sur les minéraux avec une forte teneur en U et en Th. Ces deux derniers éléments sont concentrés dans certaines phases minérales telles que l’apatite (Farley, 2000), le zircon (Tagami et al., 2003), le sphène (Reiners et Farley, 1999 ; Pik et al., 2003a) ainsi que la monazite (Gleadow et al., 2005). Le protocole de sélection des cristaux d’apatite et d’extraction de l’He ainsi que les mesures He, U et Th sont présentés en détail en Annexe 1.

II.2.3. Comportement de l’hélium

II.2.3.1. Distance d’arrêt

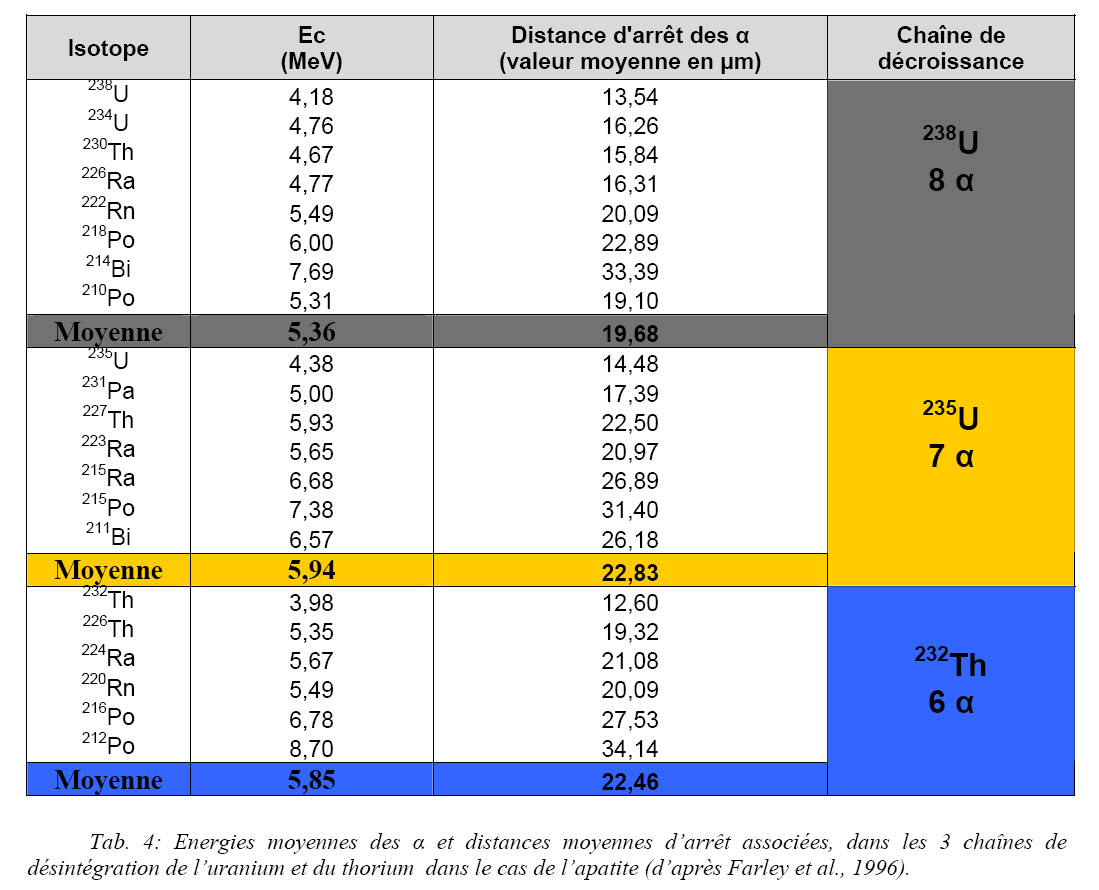
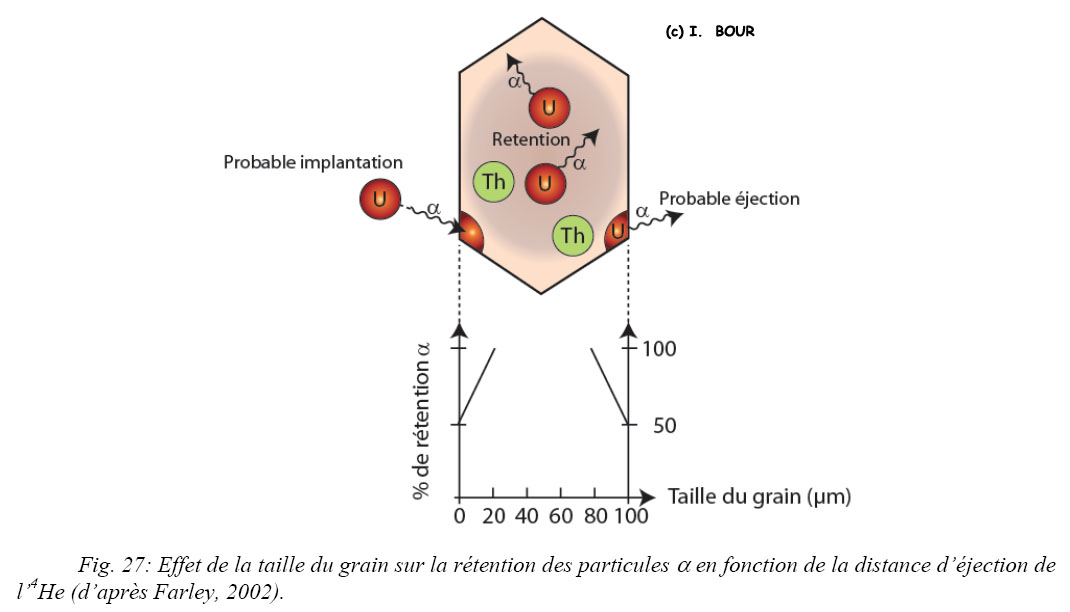
Les particules α (4He) crées sont éjectées selon une direction aléatoire et possèdent une énergie cinétique (Ec). Les particules a sont émises avec suffisamment d’énergie cinétique Ec pour pouvoir traverser la maille cristalline sur une certaine distance avant de s’immobiliser (Farley et al., 1996). Cette distance d’arrêt a été simulée à l’aide du code développé par Ziegler et al., 1985. La distance d’arrêt des α est fonction du minéral et de Ec. Cette énergie est caractéristique de chaque désintégration (Farley et al., 1996 ; Tab. 4) et  évolue dans un spectre d’énergie compris entre 4 et 8,7 MeV définissant ainsi une distance d’arrêt (stopping distance). La distance d’arrêt de l’He varie entre 12,6 et 34,1 µm dans le cas de l’apatite pour une densité de 3,2 (Tab. 4 et Fig. 26).

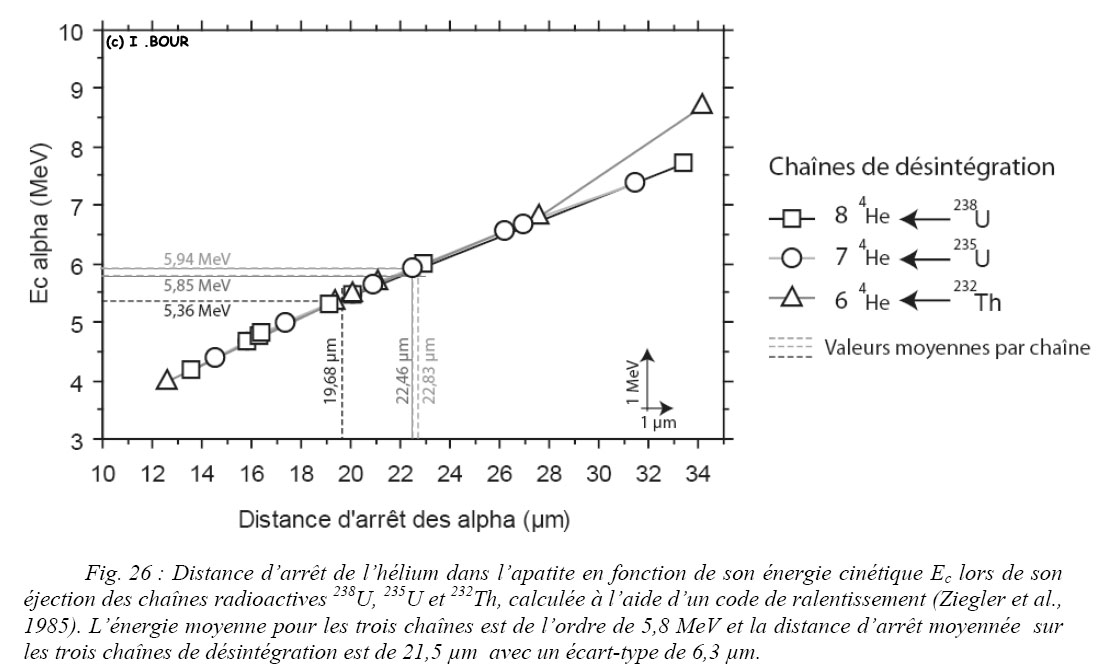
Il en résulte une perte en hélium suivant la taille du minéral et la position dans celui-ci des atomes d’U et de Th responsable de l’émission de ce gaz (Fig. 27).

La taille du grain est un paramètre important qui intervient dans la rétention de l’hélium. Dans le cas d’un atome d’uranium (ou de thorium) se situant en bordure du cristal, il en résulte la perte d’hélium par éjection. En effet, en bordure immédiate du cristal, la particule α a 50 % de probabilité d’être éjectée en dehors du cristal (Fig. 27). Il existe également, au niveau du cristal, une probabilité d’implantation des atomes d’hélium en provenance des minéraux avoisinants.

II.2.3.2. Diffusion et cinétique de diffusion standard

L’He est un gaz rare et toutes ces couches électroniques sont saturées. De part cette caractéristique atomique, l’He ne possède pas de propriété chimique. Il est donc inerte chimiquement et ne possède que des propriétés physiques, telles que la diffusion. La diffusion de l’hélium suit une loi d'Arrhenius dépendante de la température.

La loi d’Arrhenius s’écrit telle que :

La Figure 28, illustre la notion de température de fermeture (Tc) et de zone de rétention partielle de l’hélium (PRZ-He). La zone partielle de rétention (He-PRZ) est définie lorsque 10 à 90 % de l’hélium est retenu dans le cristal par rapport à la production totale (Dodson, 1986). La température de fermeture du système (Tc) correspond à la valeur à partir de laquelle la fraction d’hélium émise à l’extérieur du cristal est la même que la fraction qui est retenue. Dans cet exemple d’histoire thermique, Tc est égale 70°C.

La capacité de l’hélium à diffuser vers l’extérieur du minéral est fonction de son coefficient de diffusion contrôlé par la température. En effet, selon la température subit par le cristal au cours de son histoire, sa concentration en hélium évoluera de différentes manières (Fig. 29).

Dans le cas où la température subie par l’apatite au cours de son histoire est supérieure à sa température de fermeture pour l’hélium, le coefficient de diffusion de l’hélium est maximal (Fig. 29-A). L’hélium va se diffuser totalement à l’extérieur du cristal. Tant que T>Tc, la concentration en Hélium dans le cristal sera nulle au cours du temps.
Pour une température équivalente à la température de fermeture, la perte en hélium s’effectue par  l’éjection accompagnée d’une diffusion de ce dernier (Fig. 29-B). L’hélium s’accumule moins rapidement dans le cristal.
Si la température est inférieure à la température de fermeture, le coefficient de diffusion de l’hélium va être faible, ainsi les atomes d’hélium produits par désintégration ne vont pas diffuser à l’extérieur et vont s’accumuler dans le cristal en fonction du temps (Fig. 29-C). La perte en hélium sera causée uniquement par les phénomènes d’éjection dans la situation où des atomes pères d’U-Th se situent à une distance moyenne inférieure à 21 µm de la bordure du volume cristallin.

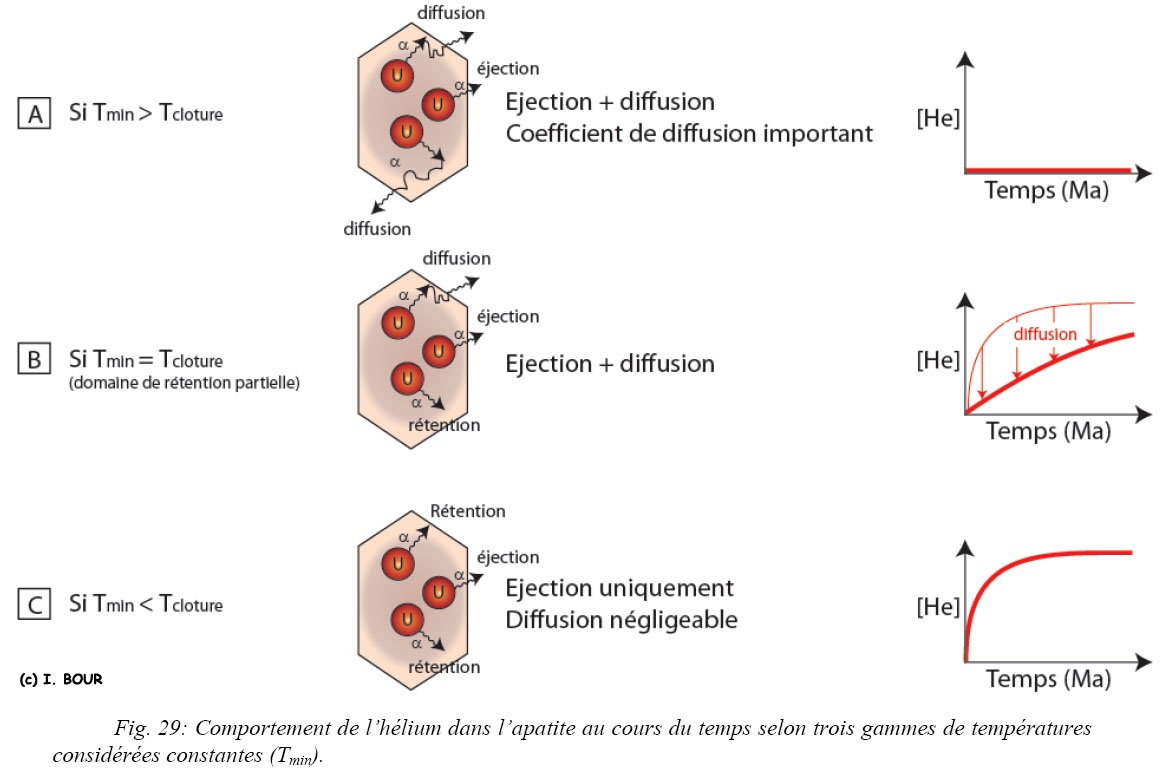
La rétention (partielle) de l’hélium est dépendante de plusieurs paramètres combinés tels que la cinétique de diffusion, la taille du cristal et notamment le taux de refroidissement correspondant au profil temps-températures, autrement dit, de l’histoire thermique.

Des paléo-zones de rétention partielle de l’hélium, définies par Wolf et al. (1998) et House et al. (1999), ont pu être mises en évidence et sont comprises entre ~40 et 70°C. La ZRP He est analogue à la zone de rétention partielle définie pour les traces de fission. Les limites de cette zone sont liées aux variations d’équilibre entre la quantité d’hélium perdue et la quantité d’hélium retenue au sein du minéral. L’accumulation de l’hélium devient totale pour des températures inférieures à 40°C (Wolf et al., 1998). Au-delà de 40°C, il s’opère une compétition entre accumulation et diffusion des particules α. Dès cette gamme de températures, l’hélium possède une énergie d’activation Ea suffisamment importante pour se déplacer de manière significative dans le minéral à l’échelle des temps géologiques. Cela aura pour conséquence la diffusion et la fuite de l’hélium hors du cristal.

Pour l’apatite, les données de diffusion montrent que la température de fermeture de l’hélium correspond à des températures de l’ordre de 60 à 75°C (Farley, 2000 ; Ehlers et al., 2003 ; Shuster et al., 2003) pour des grains dont la largeur est comprise entre 80 et 120 µm.

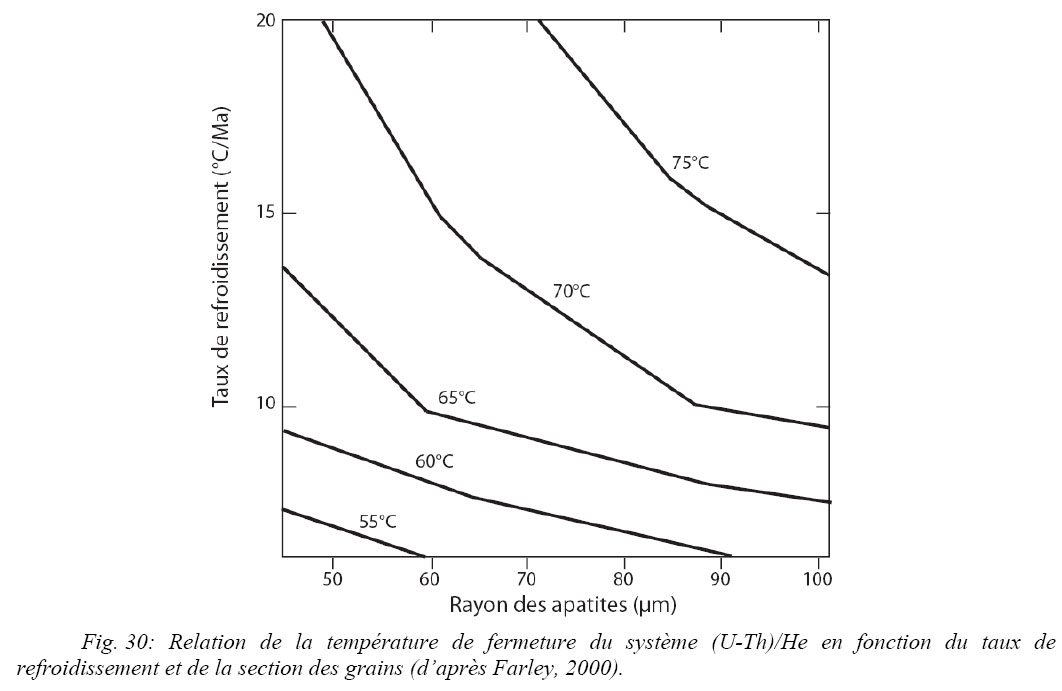
Farley, 2000 a démontré que la température de fermeture n’est pas une valeur constante et évolue en fonction de la taille des grains (Fig. 30). La température de fermeture évolue d’environ 10°C pour des tailles de grains comprises entre 50 et 100 µm en considérant une vitesse de refroidissement constante de 10°C/Ma. La température de fermeture est décroissante avec un rayon de grain plus faible. Chaque taille de grain est caractérisée par une température de fermeture.

II.2.3.4. Cinétique de diffusion prenant en compte les défauts de recul α

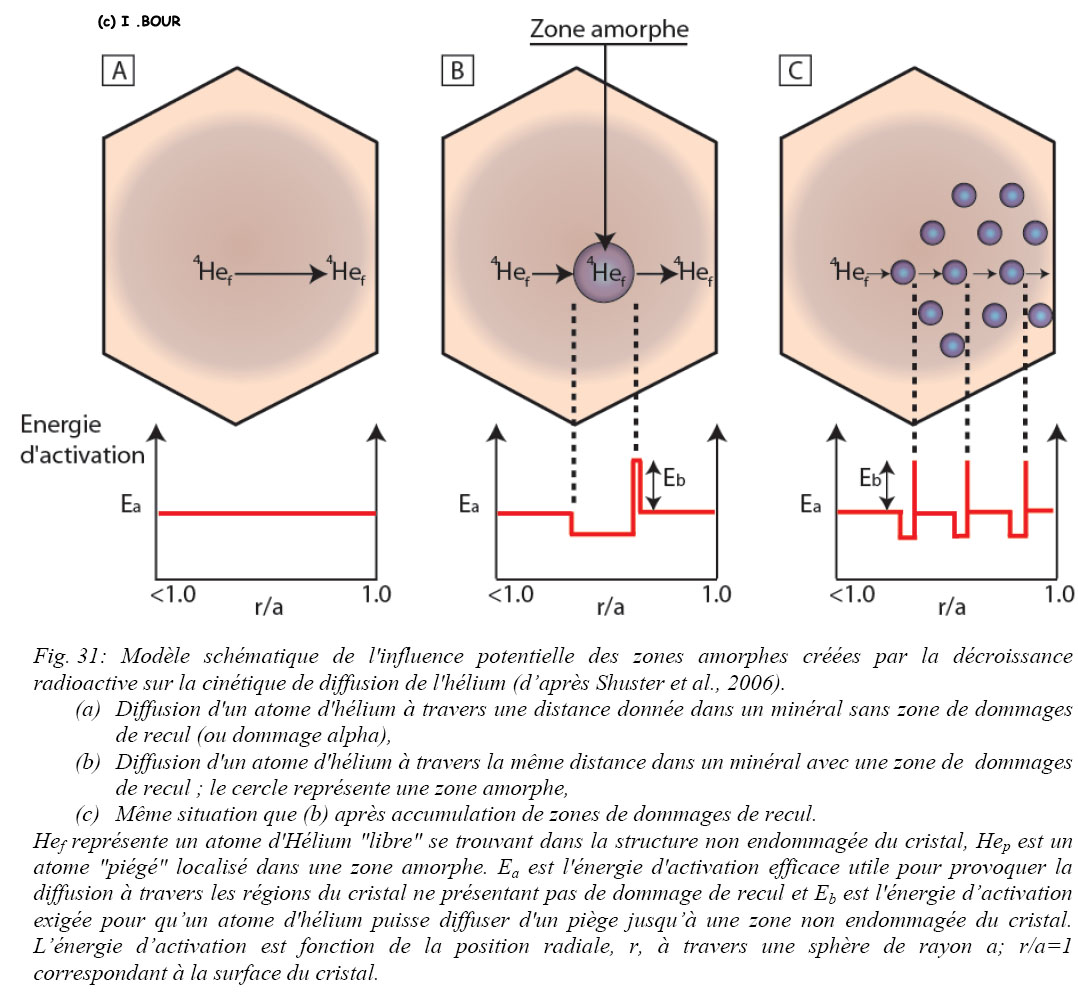
Certains auteurs ont observé que la température de fermeture de 70°C n'était pas en accord avec les données décrites précédemment (Shuster et al., 2006 ; Gautheron et al., 2009). Shuster et al. (2006) ont proposé un modèle (Fig. 31) de diffusion de l’hélium prenant en compte les effets des zones amorphes (défaut dans le réseau cristallin jouant le rôle de piège à hélium) générés par l'effet de recul des noyaux lourds lors des désintégrations alpha de l’238U, 235U et 232Th. Le modèle a été déterminé à partir d’expériences de diffusion permettant de développer une fonction mathématique qui rattache la diffusivité de l’hélium avec la température, la concentration en He ainsi que la quantité de défauts présents dans le cristal. L’insertion de cette fonction dans un modèle de production-diffusion en 4He a une conséquence sur l'interprétation des données (U-Th)/He.

L’hélium qui diffuse a tendance à rester piégé dans les zones amorphes. Celles-ci ont un effet sur la cinétique de diffusion de l’hélium dans le cristal (Farley, 2000). Il faudra donc une énergie d’activation qui soit beaucoup plus importante pour que l’hélium sorte du défaut et puisse diffuser vers le milieu extérieur. Par ce principe, à chaque fois qu’une particule a est émise, un défaut est créé et l’hélium va être de plus en plus retenu dans l’apatite. La densité de défauts augmentant au cours du temps dans le cristal, ce dernier va devenir de plus en plus rétentif à l’hélium pour une histoire thermique donnée (Shuster et al., 2006 ; Gautheron et al., 2009 ; Fig. 31).
Le rôle des défauts est important pour des températures comprises dans la zone partielle de rétention. Lorsque la température du milieu est suffisamment basse, l’énergie d’activation Ea n’est pas suffisante pour permettre la mobilité et la diffusion des particules d’hélium. Dans le cas d’une température plus conséquente, l’hélium recevra une énergie Ea qui sera suffisante pour sortir d’un site cristallin à un autre (Fig. 31-A). En prenant en compte le fait qu’il y a création de zones amorphes jouant le rôle de piège, cela nécessitera une énergie plus importante pour que l’hélium puisse ressortir des zones amorphes (Fig. 31-B, 31-C).

En tenant compte d’un changement de la cinétique de diffusion causé par la création de zone amorphe, la relation de diffusion selon la loi d’Arrhenius devient (Shuster et al., 2006) :

La rétentivité de l’hélium dans le cristal est dépendante de la valeur de l’énergie Ea + Eb.

Au-delà d’une gamme de températures, les atomes composants la structure cristalline se replacent dans leur site originel. L’évolution de la fraction de dommages α dans le temps est contrôlée par l’histoire thermique. Les zones amorphes disparaissent par recristallisation, c'est-à-dire par la réorganisation du réseau cristallin ; ceci est comparable avec les traces de fission à partir d’un certain seuil thermique et cela va avoir par conséquent une influence sur l’interprétation des âges (U-Th)/He. Des simulations de type Monte Carlo sur des cristaux d’apatite possédant une géométrie réaliste (Gautheron et al., 2009) démontrent l’effet de l’histoire thermique subi par la roche sur la fraction de dommage α contrôlant la cinétique de diffusion de l’He.

Les effets des dégâts d’irradiation sur la température de fermeture excèdent de loin les effets de la taille des grains.

La recristallisation des zones amorphes change le coefficient de diffusion d’origine ainsi que les énergies d’activation Ea et Eb. La diffusion de l’hélium selon la loi d’Arrhenius peut s’écrire en intégrant un nouveau paramètre (h) tenant compte du facteur de cicatrisation des dommages alpha (Gautheron et al., 2009).

Les paramètres t et h sont valables pour un échantillon et pour une histoire thermique donnée.

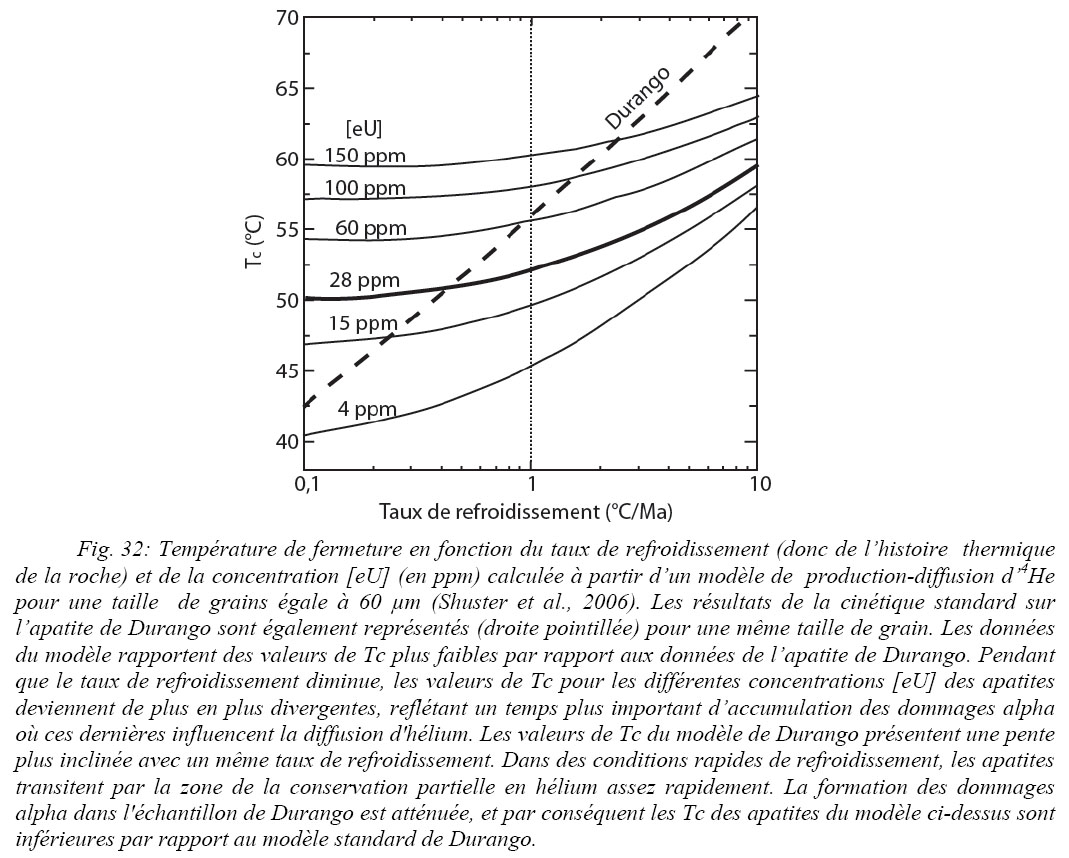
Sur un aspect chimique, le modèle de Shuster et al. (2006) (Fig. 20) et de Gautheron et al. (2009) proposent que la température de fermeture (Tc) en 4He dans l’apatite varie selon le taux de refroidissement correspondant à la vitesse d’exhumation (°C/Ma) et selon les concentrations en [U] et [Th] regroupées sous la forme d’une concentration effective en uranium [eU] ([eU] = U + 0,235 Th). Ce problème de variation de la température de fermeture est d’autant plus important pour les taux d’érosion faibles (par exemple 1°C/km soit 30 m/Ma pour un  géotherme de 30°C/km : Fig.32). Pour des concentrations [eU] de plus en plus importantes, l’écart entre l’âge mesuré et l’âge théorique tend à augmenter (Gautheron et al., 2009). La valeur de l’âge (U-Th)/He est d’autant plus importante pour des températures comprises dans la zone partielle de rétention de l’hélium. Ces résultats de simulations sont en accord avec les travaux de Shuster et al. (2006).

II.2.3.5. Facteur de correction FT

Le choix de la taille et de la morphologie appropriées des cristaux est critique pour l'obtention significative des âges (U-Th)/He. Afin de comparer l’âge des différents grains entre eux, il est nécessaire de corriger l'effet de perte d'He par éjection, dont l’effet atteint 20 à 30 %.

Dans la situation où il existe différentes tailles de grains, la comparaison des âges (U-Th)/He entre les cristaux est réalisable à la condition de les rapporter à une même géométrie permettant de simuler et de rajouter par le calcul une certaine quantité d’alpha perdue par éjection (Farley et al., 1996). La perte des α par diffusion a pour effet d’altérer l’âge réel. Une correction de l’éjection α appelée FT, qui a pour fonction d’apporter une correction aux âges He bruts obtenus, doit être déterminée.

Il existe deux façons d’estimer le facteur de correction FT. Il est déterminé soit :

• (1) par un modèle géométrique de type sphérique avec FT = 1 + A1 b + A2b² où A1 et A2 sont des paramètres spécifiques de la chaîne de désintégration radioactive de l’U et du Th et β le rapport surface/volume du cristal,
• (2) par un modèle statistique de type Monte Carlo pour des formes de cristaux quelconques mais de géométrie réaliste (identifiable) tel que : FT = nombre d’évènements triés restant dans le cristal / nombre d’évènements totaux   (FT ≤ 1). Ce modèle, plus précis et rapide à mettre en œuvre, est utilisé pour ce travail via un algorithme de simulation (Gautheron et al., 2006) disponible en ligne (http://h0.web.u-psud.fr/UThHeNe_MonteCarloSimulation). L’algorithme de fonctionnement du modèle de Monte Carlo est basé sur le tirage aléatoire d’un isotope père (U-Th) dans un volume défini du cristal échantillon. Ce tirage est suivi d’un calcul de sa position. En connaissant la distance d’arrêt des particules α, il est possible d’estimer la zone (sphère centrée sur l’élément père) dans laquelle ces particules pourront être éjectées. Le FT idéalise la géométrie 3D des cristaux, en prenant en compte des caractéristiques majeures de la géométrie.

Pour appliquer le FT à un âge (U-Th)/He brut, l’hypothèse de base est de considérer qu’il n’existe pas de zonation chimique (répartition homogène des teneurs en U et Th) dans le grain et une absence d’implantation de particules alpha pouvant provenir des minéraux voisins.

La géométrie de base des cristaux d’apatite est un prisme hexagonal (légèrement aplati dans le cas des cristaux de cette étude) surmonté d’une pyramide à chaque extrémité (Fig. 33), mais ce cas de figure n’est pas observé systématiquement. De multiples morphologies intermédiaires existent. Selon les conditions de cristallisation et de préservation, l’hexagone du cristal peut s’observer avec :

• deux terminaisons pyramidales,
• une terminaison pyramidale,
• une terminaison pyramidale et une extrémité cassée,
• des extrémités sans pyramide,
• une extrémité cassée,
• deux extrémités cassées.

La géométrie et la taille du cristal, c'est-à-dire le b, sont prises en compte lors du calcul du FT. Plus la section du grain possède une géométrie identifiable, plus la marge d’erreurs sur la mesure de l’âge sera faible (Ehlers et Farley, 2003).

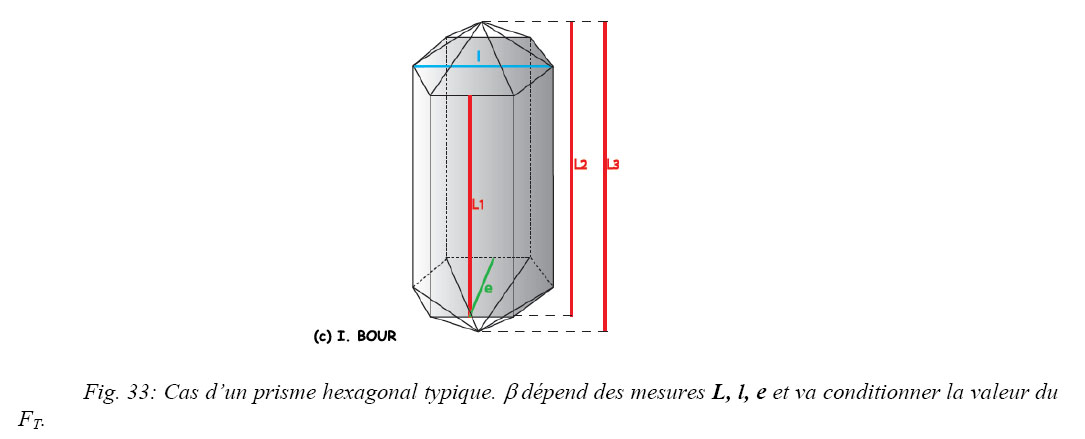
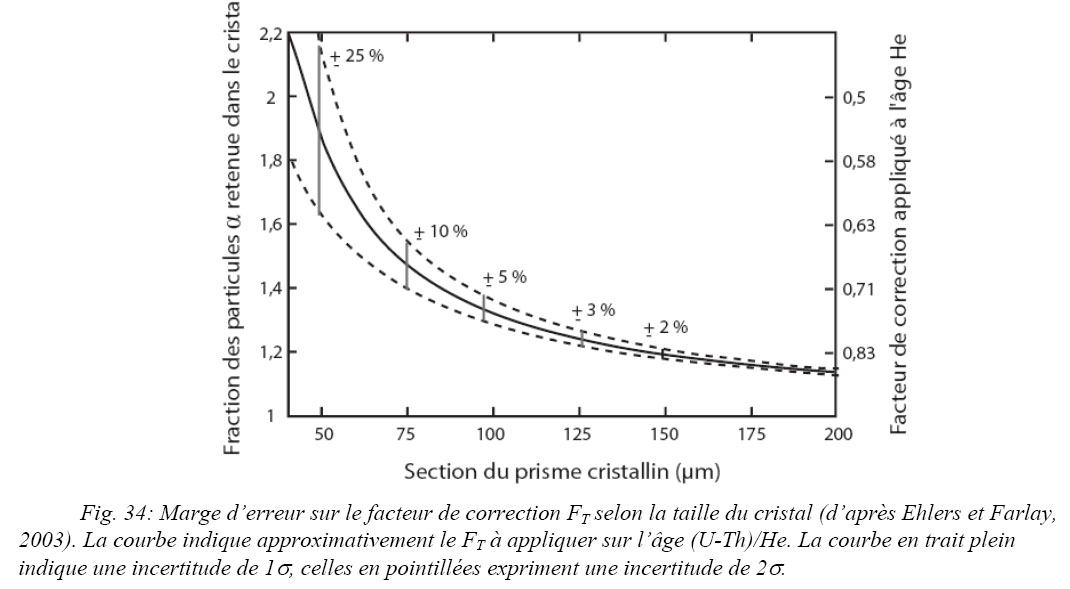
La dimension du cristal est mesurée selon sa longueur, largeur et épaisseur (Fig. 33). La taille des cristaux est le paramètre limitant. Afin d’obtenir une valeur du FT approchant de 1, la taille des grains doit être supérieure à 100 µm (Ehlers et Farley, 2003). Une erreur supérieure à 5 % est atteinte pour des cristaux de longueur inférieure à 100 µm (Fig. 34).

II.2.4. Calcul de l’âge (U-Th)/He

La mesure précise des abondances actuelles en 4He, 238U, 235U et 232Th permet d’obtenir un âge t qui correspond au temps écoulé depuis que l’4He est retenu dans le minéral. L’âge t suit la relation suivante :

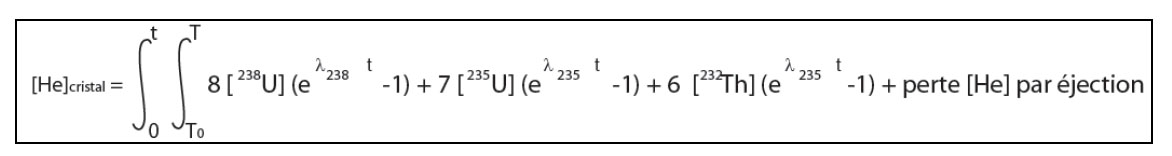
238U, 235U et 232Th sont les quantités actuelles, t représente le temps d’accumulation (âge He) et l les constantes de désintégration des isotopes concernés. Le nombre de particules a produites par chaque chaîne de désintégration est exprimé sous forme de coefficients.
Une simplification de la relation peut être effectuée en connaissant le rapport actuel des abondances isotopiques 235U/238U. Il existe 137,88 fois plus d’238U que d’235U (Steiger et Jäger, 1977) soit :

II.2.5. Significations des âges (U-Th)/He

Plusieurs auteurs ont précédemment rapporté l'évidence que les dommages de α-recul affectent la rétentivité de l’He dans l'apatite (Green et al., 2006 ; Shuster et al., 2006), y compris l’âge (U-Th)/He pour des histoires thermiques indépendamment des contraintes et des mesures directes de diffusivité.
Par conséquent, la prise en compte de l’évolution des dommages de recul α est devenue essentielle pour la méthode de datation (U-Th)/He, comme démontrée également par une étude récente de Flowers et al. (2009). Farley (2000), Shuster et al. (2006), ainsi que Gautheron et al. (2009) proposent que les défauts de recul α modifient le coefficient de diffusion efficace par un phénomène de piégeage résultant de l'équilibre chimique entre l'hélium situé dans la structure de l'apatite et les défauts.
Il a été mis en évidence une anomalie systématique entre les deux systèmes thermochronologiques (TFA et (U-Th)/He), devenant plus prononcée pour des échantillons possédant des âges stratigraphiques et TFA anciens (Green et al., 2006). Gautheron et al. (2009) décrivent ce même cas de figure sur les roches plutoniques de la bordure SE du Massif Central (avec un âge de cristallisation entre 310 et 320 Ma). Il est probable qu’un problème d’accumulation de défauts au sein des cristaux d’apatite pourrait avoir pour conséquence de piéger l’hélium dans la maille cristalline modifiant ainsi son coefficient de diffusion et surestimant ainsi la valeur de l’âge (U-Th)/He (Shuster et al., 2006 ; Flowers et al., 2007). Gautheron et al. (2009) indiquent que ce problème de diffusion de l’He apparaît lorsque l’échantillon séjourne de manière prolongée dans la zone partielle de rétention pour des températures comprises entre 80 et 40°C. L’He contenu dans le cristal ne va pas se diffuser vers le milieu extérieur en relation avec la création de défauts dans la structure cristalline générée par l’effet de recul d’atomes fils lors de la désintégration radioactive. Cette accumulation de l’He sera d’autant plus importante pour des cristaux d’apatite séjournant de manière prolongée dans la zone partielle de rétention.
Les échantillons qui ont peu subit de réchauffement vont être affectés par des phénomènes secondaires tels que des implantations, une chimie des cristaux d’apatite différente, une diffusion bloquée,…
Les âges (U-Th)/He supérieurs aux âge TFA peuvent représenter un message géologique pouvant être rapporté à un temps de résidence prolongé dans la zone partielle de rétention.